10. 如图,顺次连接四边形$ABCD$各边的中点得到四边形$A_{1}B_{1}C_{1}D_{1}$,再顺次连接四边形$A_{1}B_{1}C_{1}D_{1}$的各边中点得到四边形$A_{2}B_{2}C_{2}D_{2}$,下列说法
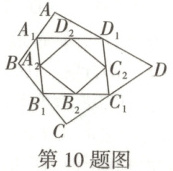
A.四边形$A_{1}B_{1}C_{1}D_{1}$一定是平行四边形
B.四边形$ABCD$的周长一定是四边形$A_{1}B_{1}C_{1}D_{1}$周长的$2$倍
C.四边形$ABCD$的面积一定是四边形$A_{2}B_{2}C_{2}D_{2}$面积的$4$倍
D.只要四边形$ABCD$的对角线相等,则四边形$A_{2}B_{2}C_{2}D_{2}$一定是矩形
错
误
的是(B
)
A.四边形$A_{1}B_{1}C_{1}D_{1}$一定是平行四边形
B.四边形$ABCD$的周长一定是四边形$A_{1}B_{1}C_{1}D_{1}$周长的$2$倍
C.四边形$ABCD$的面积一定是四边形$A_{2}B_{2}C_{2}D_{2}$面积的$4$倍
D.只要四边形$ABCD$的对角线相等,则四边形$A_{2}B_{2}C_{2}D_{2}$一定是矩形
答案:
10. B
11. 如图,$E$,$F$分别是平行四边形$ABCD$的边$AB$,$CD$上的点,$AF$与$DE$相交于点$P$,$BF$与$CE$相交于点$Q$,若$S_{\triangle APD}=a$,$S_{\triangle BQC}=b$,$S_{□ ABCD}=c$,则阴影部分的面积为(

A.$a+b$
B.$\dfrac{1}{2}c-a-b$
C.$c-2a-b$
D.$2a+b$
B
)
A.$a+b$
B.$\dfrac{1}{2}c-a-b$
C.$c-2a-b$
D.$2a+b$
答案:
11. B
12. 如图,将正方形纸片$ABCD$的$\angle B$和$\angle D$进行折叠,使两个直角的顶点重合于对角线$BD$上的点$P$处,$EF$,$GH$分别是折痕,若点$P$沿$BD$从点$B$向点$D$移动,则阴影部分的周长(
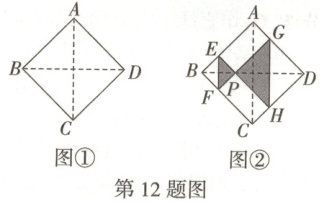
A.先变大,后变小
B.先变小,后变大
C.当点$P$在$BD$中点处时,阴影部分周长最大
D.保持不变
D
)
A.先变大,后变小
B.先变小,后变大
C.当点$P$在$BD$中点处时,阴影部分周长最大
D.保持不变
答案:
12. D
13. 新考法 条件开放 如图,在四边形$ABCD$中,$AB// CD$,$AD// BC$,在不添加任何辅助线的前提下,若使四边形$ABCD$是矩形,只需添加的一个条件是
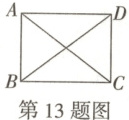
AC=BD(答案不唯一)
.
答案:
13. AC=BD(答案不唯一)
14. 如图,正六边形$ABCDEF$的边长为$6$,$M$,$N$分别为$AB$,$DE$边的中点,连接$MN$并延长交$CD$的延长线于点$P$,则$NP$的长为
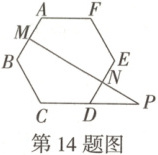
3\sqrt{3}
.
答案:
$14. 3\sqrt{3}$
15. 如图,在正方形$ABCD$和正方形$CEFG$中,点$D$在$CG$上,点$H$是$AF$的中点,若$BC=1$,$CH=3$,则$CG$的长为
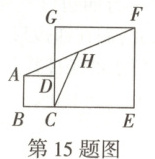
\sqrt{17}
.
答案:
$15. \sqrt{17}$
16. 如图,在四边形$ABCD$中,$AD// BC$,对角线$AC$的垂直平分线与边$AD$,$BC$分别相交于点$E$,$F$,连接$AF$,$CE$.
(1)求证:四边形$AFCE$是菱形;
(2)若$F$为$BC$的中点,$AB=6$,$AE=5$,求$AC$的长.
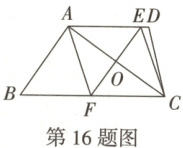
(1)求证:四边形$AFCE$是菱形;
(2)若$F$为$BC$的中点,$AB=6$,$AE=5$,求$AC$的长.

答案:
16.
(1)证明略;
(2)AC的长为8.
(1)证明略;
(2)AC的长为8.
查看更多完整答案,请扫码查看


