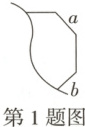
1. 图中表示被撕掉一块的正$n$边形纸片,若$a\perp b$,则$n$的值是(
A.$5$
B.$7$
C.$8$
D.$10$
C
)
A.$5$
B.$7$
C.$8$
D.$10$
答案:
1. C
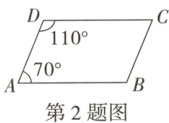
2. 如图是证明平行四边形不完整的推理过程,为保证推理成立,需在四边形$ABCD$中添加条件. 对于甲和乙添加的条件判断正确的是(
证明:$\because \angle A+\angle D=180^{\circ}$,
$\therefore AB// CD$.
$\because$.
$\therefore$四边形$ABCD$是平行四边形.
甲:$AD// BC$;乙:$AB=CD$
A.只有甲的正确
B.只有乙的正确
C.两人的都正确
D.两人的都不正确
C
)证明:$\because \angle A+\angle D=180^{\circ}$,
$\therefore AB// CD$.
$\because$.
$\therefore$四边形$ABCD$是平行四边形.
甲:$AD// BC$;乙:$AB=CD$

A.只有甲的正确
B.只有乙的正确
C.两人的都正确
D.两人的都不正确
答案:
2. C
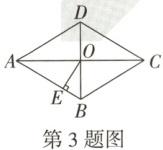
3. 如图,在菱形$ABCD$中,对角线$AC$与$BD$相交于点$O$,过点$O$作$OE\perp AB$于点$E$,若$\angle BOE=30^{\circ}$,$OB=2$,则$AO$为(
A.$2$
B.$2\sqrt{3}$
C.$4$
D.$4\sqrt{3}$
B
)
A.$2$
B.$2\sqrt{3}$
C.$4$
D.$4\sqrt{3}$
答案:
3. B
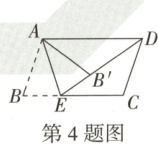
4. 如图,在$□ ABCD$中,$AD=8$,$E$为边$BC$上一点,连接$AE$,$DE$,$BE=3$,将$\triangle ABE$沿$AE$折叠,点$B$恰好落在$DE$上的点$B'$处,则$DB'$的长为(
A.$5$
B.$4.5$
C.$4$
D.$3$
A
)
A.$5$
B.$4.5$
C.$4$
D.$3$
答案:
4. A
5. 如图,将一个矩形$OABC$放在平面直角坐标系中,点$B(4,3)$,$D$,$E$分别为$OA$,$BC$上一点,将矩形沿$DE$折叠,点$B$的对应点为点$B'$,当点$A$与点$C$重合时,点$E$的坐标为(

A.$(\dfrac{25}{8},3)$
B.$(\dfrac{23}{8},3)$
C.$(-\dfrac{25}{8},3)$
D.$(-\dfrac{23}{8},3)$
A
)
A.$(\dfrac{25}{8},3)$
B.$(\dfrac{23}{8},3)$
C.$(-\dfrac{25}{8},3)$
D.$(-\dfrac{23}{8},3)$
答案:
5. A
6. 如图,正九边形$ABCDEFGHI$内接于$\odot O$,连接$AF$,$CG$,则弦$AF$,$CG$相交所成锐角的度数为(
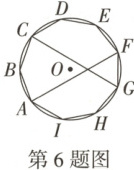
A.$45^{\circ}$
B.$54^{\circ}$
C.$60^{\circ}$
D.$72^{\circ}$
C
)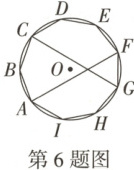
A.$45^{\circ}$
B.$54^{\circ}$
C.$60^{\circ}$
D.$72^{\circ}$
答案:
6. C
7. 如图,在$\triangle ABC$中,点$D$,$E$,$F$分别在边$BC$,$CA$,$AB$上,满足$DF// AC$,$DE// AB$,连接$AD$.
①当$DE\perp AC$时,四边形$AFDE$为矩形;
②当$AD$平分$\angle BAC$时,四边形$AFDE$为菱形;
③当$\triangle ABC$为等腰直角三角形时,四边形$AFDE$为正方形.
上述说法正确的是(

A.①②
B.①③
C.②③
D.①②③
①当$DE\perp AC$时,四边形$AFDE$为矩形;
②当$AD$平分$\angle BAC$时,四边形$AFDE$为菱形;
③当$\triangle ABC$为等腰直角三角形时,四边形$AFDE$为正方形.
上述说法正确的是(
A
)
A.①②
B.①③
C.②③
D.①②③
答案:
7. A
8. 如图,在矩形$ABCD$中,连接$AC$,分别以点$A$,$C$为圆心,以大于$\dfrac{1}{2}AC$的长为半径作弧,两弧交于点$P$,$Q$,作直线$PQ$,分别交$AB$,$CD$于点$E$,$F$,若$AB=2AD=8$,则$EF$的长为(

A.$4$
B.$8$
C.$\sqrt{5}$
D.$2\sqrt{5}$
D
)
A.$4$
B.$8$
C.$\sqrt{5}$
D.$2\sqrt{5}$
答案:
8. D
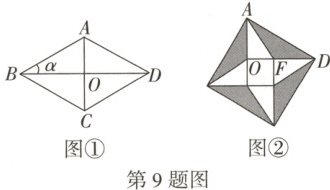
9. 最早对勾股定理进行证明的是三国时期吴国的数学家赵爽,他用一幅“赵爽弦图”极富创新意识地给出了勾股定理的证明. 如图①,将菱形$ABCD$沿对角线分成四个全等的直角三角形,将这四个直角三角形拼成如图②所示的大正方形,记阴影部分面积为$S_{1}$,空白部分面积为$S_{2}$,若$\dfrac{S_{1}}{S_{2}}=\dfrac{9}{8}$,则$\tan \alpha$的值为(
A.$\dfrac{1}{2}$
B.$\dfrac{1}{4}$
C.$\dfrac{2}{5}$
D.$\dfrac{3}{5}$
D
)
A.$\dfrac{1}{2}$
B.$\dfrac{1}{4}$
C.$\dfrac{2}{5}$
D.$\dfrac{3}{5}$
答案:
9. D
查看更多完整答案,请扫码查看


