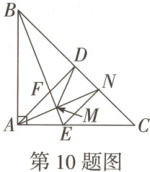
10. 如图,在等腰$Rt\triangle ABC$中,$\angle BAC = 90^{\circ}$,$AD\perp BC$于点$D$,$\angle ABC$的平分线分别交$AC$,$AD$于$E$,$F$两点,$M$为$EF$的中点,连接$AM$并延长交$BC$于点$N$。有下列说法:
甲:$\triangle AEF$是等边三角形;
乙:$AM\perp EF$;
丙:$DF = CN$。
其中说法正确的是(
A.只有甲
B.只有乙
C.只有丙
D.甲、乙、丙都不正确
甲:$\triangle AEF$是等边三角形;
乙:$AM\perp EF$;
丙:$DF = CN$。
其中说法正确的是(
B
)
A.只有甲
B.只有乙
C.只有丙
D.甲、乙、丙都不正确
答案:
10.B
11. 新考法 条件开放 如图,$BC = BE$,$\angle 1 = \angle 2$,若要使$\triangle ABE\cong\triangle DBC$,则可以添加的条件是

BA=BD(答案不唯一)
。(写出一个即可)
答案:
11.BA=BD(答案不唯一)
12. 如图,在$\triangle ABC$中,$\angle B = 30^{\circ}$,$\angle BAC = 105^{\circ}$,$AC = \sqrt{2}$,则$BC$的长为

$\sqrt {3}$+1
。
答案:
12.$\sqrt {3}$+1
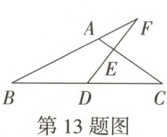
13. 万唯原创 如图,在$\triangle ABC$中,$D$是$BC$的中点,$E$是$AC$边上一点,连接$DE$并延长交$BA$的延长线于点$F$,若$DE = EF$,则$\dfrac{AF}{BF}$的值为
$\frac{1}{3}$
。
答案:
13.$\frac{1}{3}$
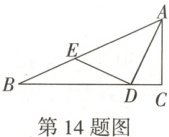
14. 万唯原创 如图,在$\triangle ABC$中,$\angle ACB = 90^{\circ}$,$D$为$BC$边上的点,连接$AD$,过点$D$作$ED\perp DA$交$AB$于点$E$,且$BE = DE$,$\dfrac{DE}{DA} = \dfrac{4}{5}$,若$AC = 20$,则$BD =$
32
。
答案:
14.32
15. 如图,$BD$平分$\angle ABC$,且$AB = BD$,连接$AD$,$CD$,$\angle C = 90^{\circ}$,过点$A$作$AF\perp BD$于点$F$。
(1)求证:$AF = CD$;
(2)若$AB = 5$,$BC = 4$,求四边形$ADCB$的周长。

(1)求证:$AF = CD$;
(2)若$AB = 5$,$BC = 4$,求四边形$ADCB$的周长。

答案:
15.
(1)证明略;
(2)四边形ADCB的周长为$12 + \sqrt {10}$
(1)证明略;
(2)四边形ADCB的周长为$12 + \sqrt {10}$
16. (2025 黑白卷)在自驾出游需要露营时,为了遮阳和防雨可以借助汽车或树木搭建如图①的“天幕”,如图②是搭建后的截面示意图,将天幕撑开,用绳子拉直天幕一侧$CE$后系在车顶$A$处,另一侧$CF$拉直后用地钉钉在地面上的点$P$处,$CD$是垂直于地面的天幕支撑杆且与点$E$,$F$所在直线垂直,可通过调整绳子所系的位置调节天幕的展开角度$\angle ECF$,已知$CE = CF$,$BD = 4.85\ m$,车顶到地面的距离为$1.7\ m$。若将“天幕”撑开到最大时天幕的展开角$\angle ECF = 150^{\circ}$,拉直$CE$所需的绳子$AE$的长为$2\ m$。(结果保留小数点后一位,参考数据:$\sin 75^{\circ}\approx 0.97$,$\cos 75^{\circ}\approx 0.26$,$\tan 75^{\circ}\approx 3.73$)
(1)求此时$\angle ACD$的度数及$CD$的长;
(2)求此时拉直$CF$所需的绳子$PF$的长。

(1)求此时$\angle ACD$的度数及$CD$的长;
(2)求此时拉直$CF$所需的绳子$PF$的长。

答案:
16.解:
(1)如解图,连接EF,过点A 作AG⊥CD于点G,则四边形ABDG为矩形,
∴∠AGC=90°,AG=BD=4.85m,DG=AB=1.7m.
∵CE=CF,CD⊥EF,
∴CD平分∠ECF
∵∠ECF=150°,
∴∠ACD=$\frac{1}{2}$∠ECF=75°.
在Rt△ACG中,
CG=$\frac{AG}{tan\angle ACG}$=$\frac{4.85}{tan75°}$≈1.30(m),
∴CD=CG+DG≈1.30+1.7=3.0(m);

(2)如解图,
∵EF⊥CD,CE=CF,
∴∠PCD=∠ACD=75°.
在Rt△CDP中,
CP=$\frac{CD}{cos\angle DCP}$=$\frac{3.0}{cos75°}$,
在Rt△ACG中,
AC=$\frac{AG}{sin\angle ACG}$=$\frac{4.85}{sin75°}$.
∵AE=2,
∴CE=CF=AC - AE=$\frac{4.85}{sin75°}$ - 2,
∴PF=CP - CF=$\frac{3.0}{cos75°}$ - ($\frac{4.85}{sin75°}$ - 2)≈8.5(m).
答:此时拉直CF所需的绳子PF 的长约为8.5m.
16.解:
(1)如解图,连接EF,过点A 作AG⊥CD于点G,则四边形ABDG为矩形,
∴∠AGC=90°,AG=BD=4.85m,DG=AB=1.7m.
∵CE=CF,CD⊥EF,
∴CD平分∠ECF
∵∠ECF=150°,
∴∠ACD=$\frac{1}{2}$∠ECF=75°.
在Rt△ACG中,
CG=$\frac{AG}{tan\angle ACG}$=$\frac{4.85}{tan75°}$≈1.30(m),
∴CD=CG+DG≈1.30+1.7=3.0(m);

(2)如解图,
∵EF⊥CD,CE=CF,
∴∠PCD=∠ACD=75°.
在Rt△CDP中,
CP=$\frac{CD}{cos\angle DCP}$=$\frac{3.0}{cos75°}$,
在Rt△ACG中,
AC=$\frac{AG}{sin\angle ACG}$=$\frac{4.85}{sin75°}$.
∵AE=2,
∴CE=CF=AC - AE=$\frac{4.85}{sin75°}$ - 2,
∴PF=CP - CF=$\frac{3.0}{cos75°}$ - ($\frac{4.85}{sin75°}$ - 2)≈8.5(m).
答:此时拉直CF所需的绳子PF 的长约为8.5m.
查看更多完整答案,请扫码查看


