《2025年课堂精练五年级数学上册北师大版》

4. 李老师把 $32$ 本作业本平均分给一些同学(人数不止一个),正好分完。同学的人数有多少种可能? 分别是多少?

答案： 5 种可能,分别是2,4,8,16,32。

5. $48$ 个同学列队参加体操表演,列队时要求每行人数相同。有哪些排法? (每行至少 $2$ 人,至少排 $2$ 列)

答案： 2行,每行24人;3行,每行16人;4行,每行12人;6行,每行8人;8行,每行6人;12行,每行4人;16行,每行3人;24行,每行2人。

6. 要把 $40$ 支笔装在礼品盒里,使得每个盒子装得同样多,有哪些装法? 每种装法各需要几个盒子? 如果有 $41$ 支笔呢?

答案： 每盒1支,共40盒;每盒2支,共20盒;每盒4支,共10盒;每盒5支,共8盒;每盒8支,共5盒;每盒10支,共4盒;每盒20支,共2盒;每盒40支,共1盒。每盒1支,共41盒;每盒41支,共1盒。

7. 把这两根铁丝截成完全相等的小段,可以截成哪些整厘米数的长度? 请写出你的思考过程。

答案： 1 cm,2 cm,4 cm,8 cm 思考过程略

8. 把一块长 $100 cm$、宽 $60 cm$ 的长方形纸板剪成同样大小的正方形纸板,要使剪成的正方形尽量大且无剩余,正方形的边长应是多少厘米?

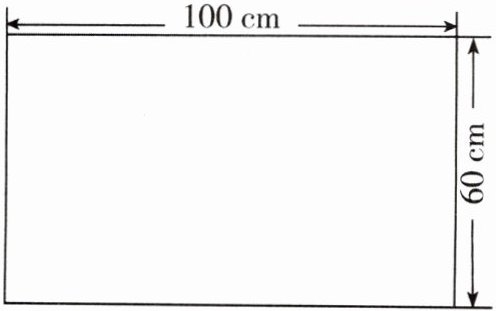
答案： 20 cm
要使剪成的正方形尽量大且无剩余，正方形的边长应是100和60的最大公因数。
$100=2×2×5×5$
$60=2×2×3×5$
最大公因数为$2×2×5=20$