《2025年课堂精练五年级数学上册北师大版》

4. 以虚线为对称轴,分别画出下面各点的对称点。

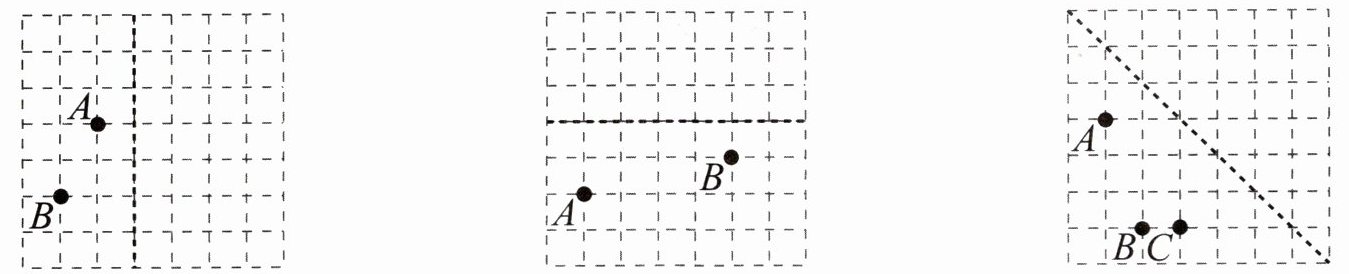
答案： 本题可根据轴对称的性质来画出各点的对称点，轴对称的性质为：对称轴是对称点连线的垂直平分线，即对称点到对称轴的距离相等。
对于第一组点（以竖直虚线为对称轴）
点$A$：点$A$到竖直虚线的水平距离为$2$格，那么它关于竖直虚线的对称点到竖直虚线的水平距离也为$2$格，且在竖直虚线的右侧，据此可画出$A$的对称点。
点$B$：点$B$到竖直虚线的水平距离为$3$格，那么它关于竖直虚线的对称点到竖直虚线的水平距离也为$3$格，且在竖直虚线的右侧，据此可画出$B$的对称点。
对于第二组点（以水平虚线为对称轴）
点$A$：点$A$到水平虚线的垂直距离为$3$格，那么它关于水平虚线的对称点到水平虚线的垂直距离也为$3$格，且在水平虚线的上方，据此可画出$A$的对称点。
点$B$：点$B$到水平虚线的垂直距离为$1$格，那么它关于水平虚线的对称点到水平虚线的垂直距离也为$1$格，且在水平虚线的上方，据此可画出$B$的对称点。
对于第三组点（以倾斜虚线为对称轴）
点$A$：过点$A$作倾斜虚线的垂线，测量点$A$到倾斜虚线的距离，然后在倾斜虚线的另一侧取相同距离的点，即为$A$的对称点。
点$B$：过点$B$作倾斜虚线的垂线，测量点$B$到倾斜虚线的距离，然后在倾斜虚线的另一侧取相同距离的点，即为$B$的对称点。
点$C$：过点$C$作倾斜虚线的垂线，测量点$C$到倾斜虚线的距离，然后在倾斜虚线的另一侧取相同距离的点，即为$C$的对称点。
按照上述方法，即可画出各点关于虚线的对称点（由于无法直接绘制图形，你可根据上述步骤在给定的图中进行绘制）。

5. 画出下面图形关于虚线对称的图形。

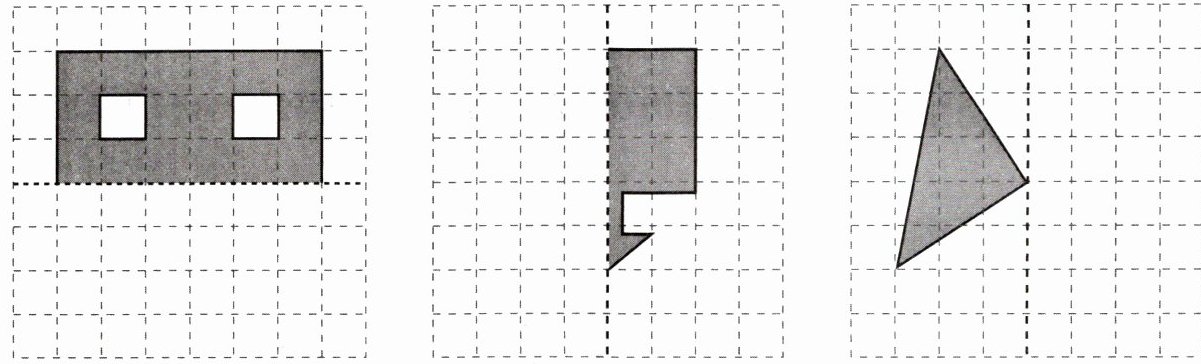
答案： 本题可根据轴对称图形的性质，通过找出原图形关键点关于虚线的对称点，再连接对称点来画出对称图形。
步骤一：明确轴对称图形的性质
在平面内，如果一个图形沿一条直线折叠，直线两旁的部分能够完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴。对于一个图形来说，其关于某条直线对称的图形，对应点所连的线段被对称轴垂直平分。
步骤二：分别找出三个图形关键点关于虚线的对称点
第一个图形**：这是一个带有两个小正方形缺口的大长方形，以水平虚线为对称轴。先找出大长方形的四个顶点以及两个小正方形的顶点关于水平虚线的对称点。例如大长方形的顶点，设原顶点坐标（假设以网格左下角为原点建立坐标系），根据对称点到对称轴距离相等的性质，求出对称点坐标。
第二个图形**：这是一个不规则图形，以垂直虚线为对称轴。找出该图形的各个顶点（包括缺口处的顶点）关于垂直虚线的对称点。比如图形的拐角顶点、缺口顶点等，依据对称点的性质确定其对称点位置。
第三个图形**：这是一个三角形，以垂直虚线为对称轴。找出三角形的三个顶点关于垂直虚线的对称点，同样根据对称点到对称轴距离相等来确定。
步骤三：连接对称点
第一个图形**：将求出的大长方形对称点以及小正方形对称点依次连接起来，就得到关于水平虚线对称的图形。
第二个图形**：把各个顶点的对称点按照原图形的连接顺序连接，形成关于垂直虚线对称的图形。
第三个图形**：连接三角形三个顶点的对称点，得到关于垂直虚线对称的三角形。
最终画出的对称图形如下（由于无法直接绘制图形，你可根据上述步骤自行绘制）：
第一个图形：与原大长方形上下对称，小正方形缺口位置也相应对称。
第二个图形：与原不规则图形左右对称，缺口位置也左右对称。
第三个图形：与原三角形左右对称。
综上，按照上述方法可画出给定图形关于虚线对称的图形。

6. 看一看,想一想,如何把“∃”变成“E”,“W”变成“M”？在图上画一画。

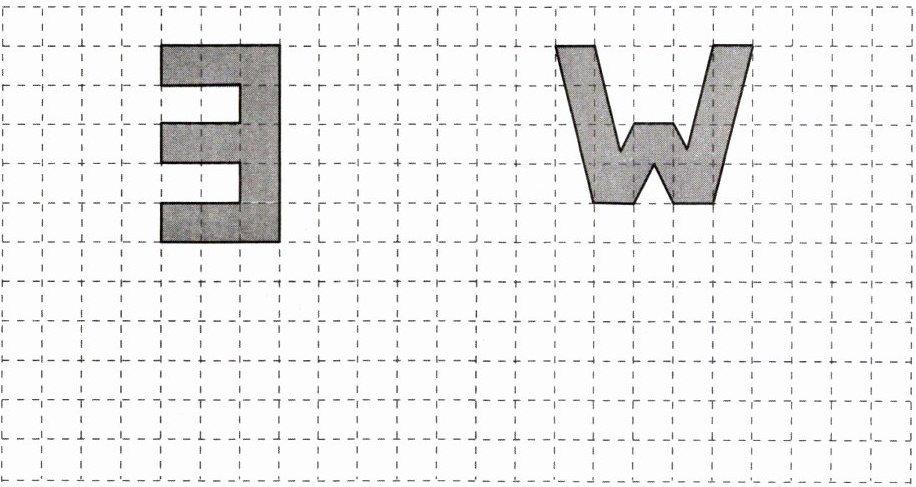
答案： 本题可通过轴对称的性质，画出图形的另一半，从而将“∃”变成“E”，“W”变成“M”。
步骤一：将“∃”变成“E”
根据轴对称图形的定义：如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴。
“∃”关于某条水平直线对称，画出它的对称图形，即可得到“E”。具体画法为：以“∃”最上面横线所在直线为对称轴，画出“∃”下半部分关于该对称轴的对称图形 。
步骤二：将“W”变成“M”
同理，“W”也关于某条水平直线对称，画出它的对称图形，就能得到“M”。具体画法为：以“W”中间凹陷处所在水平直线为对称轴，画出“W”上半部分关于该对称轴的对称图形 。
综上，按照上述方法在图上画出对应图形（具体图形需根据上述原理在给定方格图中绘制）。

7. 在下面的方格纸上各设计一个轴对称图形。

答案： 本题可根据轴对称图形的定义，在方格纸上设计出符合要求的图形。
步骤一：明确轴对称图形的定义
如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴。
步骤二：设计轴对称图形
对于左边方格纸（以中间竖线为对称轴）：可以画一个等腰三角形，先在对称轴左边确定三角形的两个顶点，比如在对称轴左边第二行第二列和第四行第二列确定两个点，然后根据对称性质，在对称轴右边第二行第二列和第四行第二列的对称位置（即第二行第六列和第四行第六列）确定另外两个顶点，连接这三个点就得到一个以中间竖线为对称轴的等腰三角形轴对称图形。
对于右边方格纸（以中间横线为对称轴）：可以画一个等腰梯形，先在对称轴上方确定梯形的两个顶点，比如在对称轴上方第二行第二列和第二行第六列确定两个点，再在对称轴下方第二行第二列和第二行第六列的对称位置（即第六行第二列和第六行第六列）确定另外两个顶点，连接这四个点就得到一个以中间横线为对称轴的等腰梯形轴对称图形。
（答案不唯一，只要设计的图形符合轴对称图形的定义即可）

8. 如图,在下面各图中再涂黑一个小正方形,得到一个轴对称图形,试一试。

答案： 1. 涂黑C
2. 涂黑F
3.涂黑B
4.涂黑D
5.涂黑E