第23页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
5. 以下图形分别有几条对称轴?画一画,填一填。


1、2、4、1、2
答案:
本题可根据对称轴的定义,分别分析每个图形的对称轴数量。
第一个图形(类似等腰三角形):
根据对称轴的定义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴。
该图形沿着其顶点到底边中点的连线对折后,两部分完全重合,所以它有$1$条对称轴。
第二个图形(长方形):
长方形沿其长的中点连线对折或沿其宽的中点连线对折,两部分都能完全重合,所以长方形有$2$条对称轴。
第三个图形(正方形):
正方形沿其对边中点连线对折(有$2$条),沿其两条对角线对折(有$2$条),两部分都能完全重合,所以正方形有$4$条对称轴。
第四个图形(等腰梯形):
等腰梯形沿着上下底中点的连线对折后,两部分完全重合,所以它有$1$条对称轴。
第五个图形(菱形):
菱形沿其两条对角线对折后,两部分完全重合,所以它有$2$条对称轴。
综上,答案依次为$\boldsymbol{1}$、$\boldsymbol{2}$、$\boldsymbol{4}$、$\boldsymbol{1}$、$\boldsymbol{2}$。
第一个图形(类似等腰三角形):
根据对称轴的定义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴。
该图形沿着其顶点到底边中点的连线对折后,两部分完全重合,所以它有$1$条对称轴。
第二个图形(长方形):
长方形沿其长的中点连线对折或沿其宽的中点连线对折,两部分都能完全重合,所以长方形有$2$条对称轴。
第三个图形(正方形):
正方形沿其对边中点连线对折(有$2$条),沿其两条对角线对折(有$2$条),两部分都能完全重合,所以正方形有$4$条对称轴。
第四个图形(等腰梯形):
等腰梯形沿着上下底中点的连线对折后,两部分完全重合,所以它有$1$条对称轴。
第五个图形(菱形):
菱形沿其两条对角线对折后,两部分完全重合,所以它有$2$条对称轴。
综上,答案依次为$\boldsymbol{1}$、$\boldsymbol{2}$、$\boldsymbol{4}$、$\boldsymbol{1}$、$\boldsymbol{2}$。
6. 画出下面图形的全部对称轴。


答案:
本题可根据对称轴的定义,通过对折图形判断对称轴的数量和位置。
对称轴是指使几何图形沿着某条直线对折后,直线两侧的部分能够完全重合的直线。
第一个图形**:
通过观察和尝试对折,可发现该图形有$1$条对称轴,为过图形上下顶点的直线。
第二个图形**:
经分析,此图形有$2$条对称轴,分别为水平方向过图形中心的直线和垂直方向过图形中心的直线。
第三个图形**:
该图形没有对称轴,因为无论沿哪条直线对折,直线两侧的部分都不能完全重合。
第四个图形**:
此图形有$1$条对称轴,为过图形上下顶点的直线。
综上,按照上述分析画出对应图形的对称轴即可(因无法直接绘制图形,故以文字描述对称轴位置)。
对称轴是指使几何图形沿着某条直线对折后,直线两侧的部分能够完全重合的直线。
第一个图形**:
通过观察和尝试对折,可发现该图形有$1$条对称轴,为过图形上下顶点的直线。
第二个图形**:
经分析,此图形有$2$条对称轴,分别为水平方向过图形中心的直线和垂直方向过图形中心的直线。
第三个图形**:
该图形没有对称轴,因为无论沿哪条直线对折,直线两侧的部分都不能完全重合。
第四个图形**:
此图形有$1$条对称轴,为过图形上下顶点的直线。
综上,按照上述分析画出对应图形的对称轴即可(因无法直接绘制图形,故以文字描述对称轴位置)。
7.  照左图,在一张对折了的纸上打一个小圆孔,展开后的样子是(
照左图,在一张对折了的纸上打一个小圆孔,展开后的样子是(

 照左图,在一张对折了的纸上打一个小圆孔,展开后的样子是(
照左图,在一张对折了的纸上打一个小圆孔,展开后的样子是(B
)。(填字母)
答案:
B
8. 将纸像这样对折后, 像下面四幅图那样沿虚线剪下,剩下的纸打开后是什么图形?与第二行的图形连一连。
像下面四幅图那样沿虚线剪下,剩下的纸打开后是什么图形?与第二行的图形连一连。
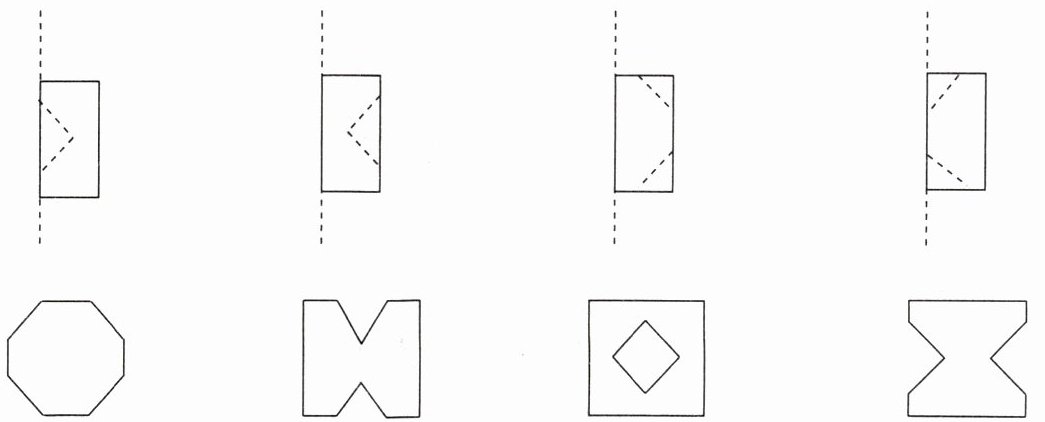
 像下面四幅图那样沿虚线剪下,剩下的纸打开后是什么图形?与第二行的图形连一连。
像下面四幅图那样沿虚线剪下,剩下的纸打开后是什么图形?与第二行的图形连一连。
答案:
第一行从左到右依次连第二行第三、二、一、四图
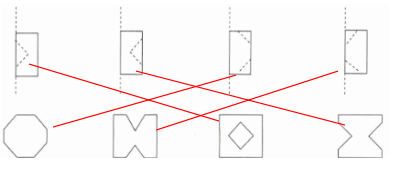
第一行从左到右依次连第二行第三、二、一、四图

9. 数的计算中也有一些有趣的对称形式,如$12×231 = 132×21$。仿照这样的形式填空,并检查等式是否成立。
(1)$18×8181 = $(
(1)$18×8181 = $(
1818
)×(81
) (2)$102×402 = $(204
)×(201
)
答案:
(1)18×8181=1818×81
(2)102×402=204×201
(1)18×8181=1818×81
(2)102×402=204×201
查看更多完整答案,请扫码查看


