《2025年同步练习册智慧拓展六年级数学上册人教版菏泽专版》

1. 根据下面的描述,在平面图上标出各个场所的位置。
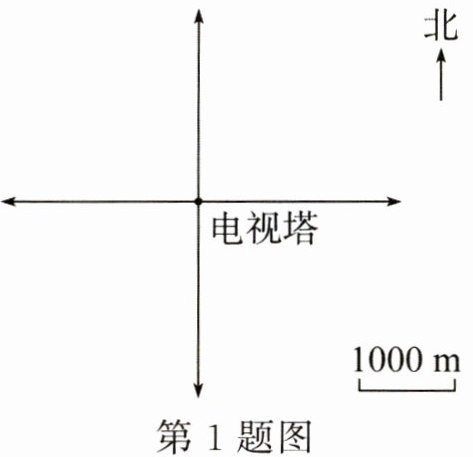
(1) 医院在电视塔的北偏东$45^{\circ}方向1$km 处。
(2) 超市在电视塔的西偏南$30^{\circ}方向1500$m 处。
(3) 实验小学在电视塔的西偏北$20^{\circ}方向2$km 处。

答案： （1）因为图上1厘米代表实际距离1000米，1000米 = 1000m，1÷1000 = 0.001（米）=1（厘米），所以在平面图上，以电视塔为观测点，在北偏东$45^{\circ}$方向画1厘米长的线段，标出医院。
（2）1500÷1000 = 1.5（厘米），以电视塔为观测点，在西偏南$30^{\circ}$方向画1.5厘米长的线段，标出超市。
（3）2km = 2000m，2000÷1000 = 2（厘米），以电视塔为观测点，在西偏北$20^{\circ}$方向画2厘米长的线段，标出实验小学。
（在给出的平面图中按上述操作画出对应位置）。

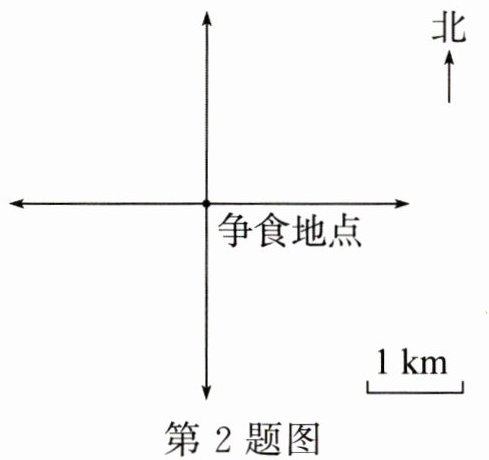
2. 某天通过卫星定位到非洲草原上一只猎豹和一头狮子在争夺食物。它们突然受到惊吓,猎豹以每分钟$2$km 的速度向西偏南$30^{\circ}$的方向奔跑,狮子以每分钟$1$km 的速度向东偏北$40^{\circ}$的方向奔跑。请你在图中标出$1.5$分钟后它们的位置。

答案： 1. 猎豹奔跑距离：$2×1.5 = 3\,km$，方向：西偏南$30^{\circ}$，在图中从争食地点沿西偏南$30^{\circ}$方向画$3\,cm$（比例尺$1\,cm=1\,km$）线段确定位置。
2. 狮子奔跑距离：$1×1.5 = 1.5\,km$，方向：东偏北$40^{\circ}$，在图中从争食地点沿东偏北$40^{\circ}$方向画$1.5\,cm$线段确定位置。

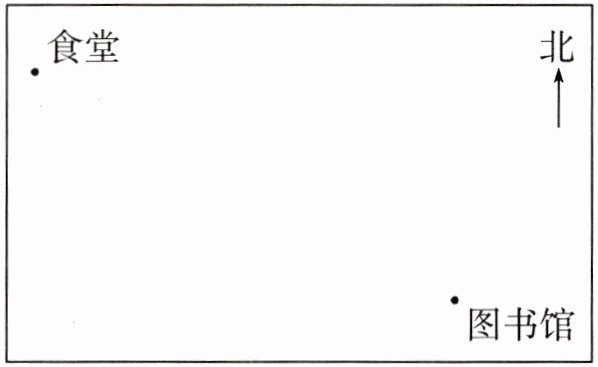
3. 如图是某小学的平面图,原来上面标有教学楼、图书馆和食堂的位置,后来平面图被污染了,教学楼的位置看不清了,现在只知道教学楼在食堂的南偏东$40^{\circ}$方向上,在图书馆的西偏北$20^{\circ}$方向上。请你在平面图上标出教学楼的位置。

答案： 1. 以食堂为观测点：
在食堂处建立方向标，根据教学楼在食堂的南偏东$40^{\circ}$方向，用量角器在食堂南偏东$40^{\circ}$方向画一条射线。
2. 以图书馆为观测点：
在图书馆处建立方向标，根据教学楼在图书馆的西偏北$20^{\circ}$方向，用量角器在图书馆西偏北$20^{\circ}$方向画一条射线。
3. 两条射线的交点即为教学楼的位置，在交点处标上“教学楼”。

4. 书店在娜娜家北偏西$30^{\circ}$方向上,距离娜娜家$4$km；超市在娜娜家西偏北$30^{\circ}$方向上,与娜娜家的距离也是$4$km。

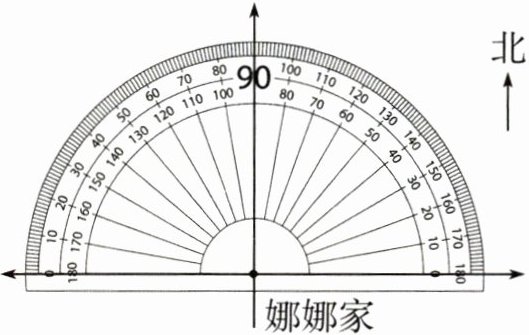
(1) 根据上面的描述,借助图上的量角器,在平面图上标出书店和超市的位置。要求用$1$cm 长的线段表示$1$km,并保留书店与娜娜家、超市与娜娜家的连线。
(2) 通过推理可知,书店在超市的(东)偏(南)(30)$^{\circ}$方向上。

答案： 1. （1）
因为$1cm$长的线段表示$1km$，书店距离娜娜家$4km$，则图上距离为$4cm$；超市距离娜娜家$4km$，图上距离也为$4cm$。
以娜娜家为顶点，根据“北偏西$30^{\circ}$”，用量角器量出$30^{\circ}$，在这个方向上画一条$4cm$长的线段表示书店的位置；根据“西偏北$30^{\circ}$”，用量角器量出$30^{\circ}$，在这个方向上画一条$4cm$长的线段表示超市的位置。
2. （2）
解：连接书店、超市和娜娜家，得到一个等边三角形（因为书店与娜娜家距离、超市与娜娜家距离都是$4km$，书店与超市的距离也为$4km$）。
书店在超市的东偏南$30^{\circ}$方向上。
故答案依次为：东；南；$30$。