《2025年新编基础训练九年级数学上册人教版》

6. 如图,△ABC与△DEC关于点C成中心对称,AB= $\sqrt{5}$,AE= 3,∠D= 90°,则AC等于(A)

A.1
B.2
C.3
D.4

答案： A

7. 如图,将△ABC以点O为旋转中心旋转180°后得到△A′B′C′.ED是△ABC的中位线,经旋转后变为线段E′D′.已知BC= 4,则线段E′D′的长度为(A)

A.2
B.3
C.4
D.1.5

答案： A

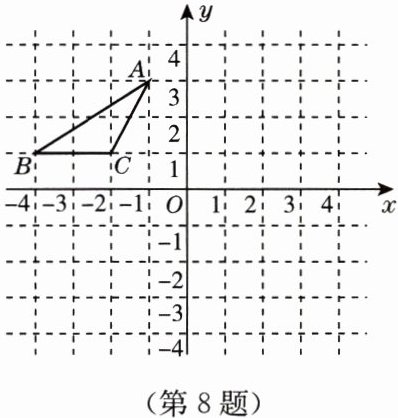
8. 如图,△ABC三个顶点的坐标分别为A(-1,3),B(-4,1),C(-2,1).
(1)请画出△ABC向右平移5个单位长度后得到的$△A_1B_1C_1；$
(2)请画出△ABC关于原点对称的$△A_2B_2C_2；$
(3)求四边形$ABA_2B_2$的面积.

答案：
解:
(1)如图,△A₁B₁C₁即为所求.
　　　　　　
(2)如图,△A₂B₂C₂即为所求.
(3)如图,四边形ABA₂B₂的面积=8×6-($\frac{1}{2}$×2×3+$\frac{1}{2}$×4×5+$\frac{1}{2}$×2×3+$\frac{1}{2}$×4×5)=22.
解后反思:网格中的图形,运用和差法或割补法可计算其面积,比如问题
(3)中,我们通过补图进行求解,最后计算面积的和差得到答案.

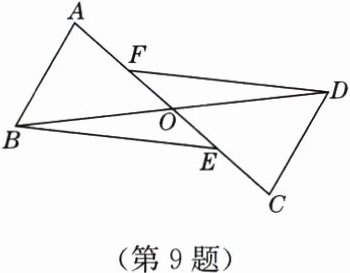
9. 如图,△ABO与△CDO关于点O成中心对称,点E,F在线段AC上,且AF= CE,求证：DF= BE.

答案： 证明:
∵△ABO与△CDO关于点O成中心对称,
∴BO=DO,AO=CO.
∵AF=CE,
∴AO - AF=CO - CE,
∴FO=EO.在△FOD和△EOB中,$\left\{\begin{array}{l}FO=EO,\\ ∠FOD=∠EOB,\\ DO=BO,\end{array}\right.$
∴△FOD≌△EOB(SAS),
∴DF=BE.

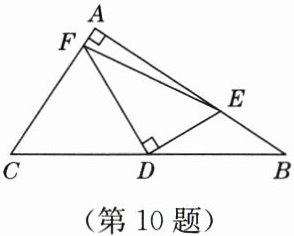
10. 如图,在△ABC中,∠A= 90°,点D为BC的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,试写出线段BE,EF,FC之间的数量关系,并说明理由.

答案：
解:FC²+BE²=EF².理由如下:作△BDE关于点D成中心对称的△CDM,连接FM,如图所示.
　　　　　　　
∵点D为BC的中点,
∴BD=CD.由中心对称的性质可得CM=BE,MD=ED,∠DCM=∠B.又
∵∠B+∠ACB=90°,
∴∠DCM+∠ACB=90°,即∠FCM=90°.在△FME中,MD=ED,FD⊥ME,
∴FM=FE.又
∵在Rt△FCM中,FC²+CM²=FM²,
∴FC²+BE²=EF².
解析:通过几何图形的中心对称变换,可以将线段进行等长的位置转移,使分散的几何元素集中起来.