《2025年新编基础训练九年级数学上册人教版》

1. 等号两边都是整式,只含有一个未知数,并且未知数的最高次数是2的方程,叫做一元二次方程.

答案： 一；2

4. 在某次集会中,参加集会的每两人都握一次手,一共握了66次手,求有多少人参加这次集会. 设有$x$人参加这次集会,则列方程为$\frac{1}{2}x(x-1)=66$.

答案： $\frac{1}{2}x(x-1)=66$

1. 下列方程：①$3x^{2}+x= 20$；②$2x^{2}-3xy+4= 0$；③$x^{2}-\frac{1}{x}= 4$；④$x^{2}-3x= 4$；⑤$x^{2}-\frac{x}{3}+3= 0$. 一元二次方程共有(B)
A.2个
B.3个
C.4个
D.5个

答案： B

2. 若方程$(a + 1)x^{2}-2x - 1 = 0是关于x$的一元二次方程,则$a$满足的条件是(B)
A.$a\neq0$
B.$a\neq - 1$
C.$a＞ - 1$
D.$a＜ - 1$

答案： B

3. 将关于$x的一元二次方程x^{2}+x - 1 = 2(x - 3)$化成一般形式后,一次项系数和常数项分别为(B)
A.$1$,$-4$
B.$-1$,$5$
C.$-1$,$-5$
D.$1$,$-6$

答案： B

4. 把一元二次方程$(x + 1)(1 - x)= 2x$化成二次项系数大于0的一般形式是$x^{2}+2x-1=0$.

答案： $x^{2}+2x-1=0$

5. 以$-2$为根的一元二次方程是(D)
A.$x^{2}-x + 2 = 0$
B.$x^{2}-x - 2 = 0$
C.$x^{2}+x + 2 = 0$
D.$x^{2}+x - 2 = 0$

答案： D

6. 方程$2x - 4 = 0的解也是关于x的方程x^{2}+mx + 2 = 0$的一个解,则$m$的值为-3.

答案： -3 解析：解$2x-4=0$，得$x=2$.把$x=2$代入方程$x^{2}+mx+2=0$，得$4+2m+2=0$，解得$m=-3$.

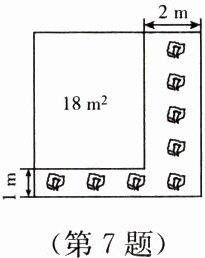
7. (生活情境)某公园有一块正方形的空地,后来从这块空地上划出部分区域栽种鲜花(如图),原空地一边减少了$1m$,另一边减少了$2m$,剩余空地的面积为$18m^{2}$,求原正方形空地的边长. 设原正方形空地的边长为$x m$,则可列方程为$(x-1)(x-2)=18$.

答案： $(x-1)(x-2)=18$