4. 当 $ x = -1 $ 时,代数式 $ 2ax^{3} - 3bx + 8 $ 的值为 $ 18 $,则代数式 $ 3b - 2a + 2 $ 的值为
12
。
答案:
12
5. 图中阴影部分的面积为
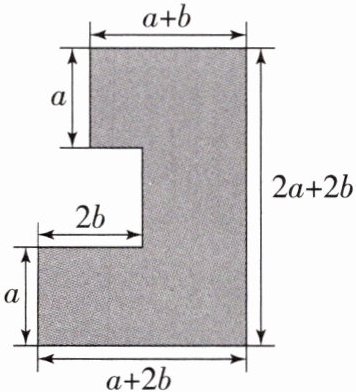
2a²+5ab
(用代数式表示)。
答案:
解析:阴影部分的面积为(a+2b)(2a+2b)-2b·2b-ab=2a²+2ab+4ab+4b²-4b²-ab=2a²+5ab.答案:2a²+5ab
6. 一列代数式:$ -x^{2} $,$ 3x^{3} $,$ -5x^{4} $,$ 7x^{5} $,…,按此规律排列,则第 $ 7 $ 个代数式为
-13x⁸
。
答案:
-13x⁸
7. 某单位计划加工一批零件,每天加工的件数与加工的天数之间的关系如下表:
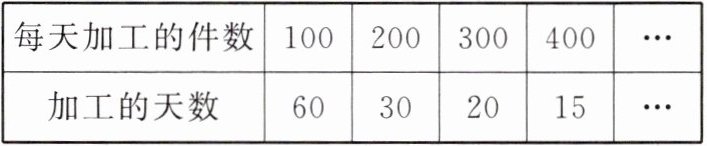
(1) 这批零件共有多少件?
(2) 加工的天数是怎样随着每天加工的件数的变化而变化的?
(3) 用 $ y $ 表示加工的天数,用 $ x $ 表示每天加工的件数,用式子表示 $ y $ 与 $ x $ 的关系。$ y $ 与 $ x $ 成什么比例关系?
(1)100×60=6 000(件).答:这批零件共有6 000件.
(2)加工的天数随着每天加工的件数的变大而变小,而且加工的天数与每天加工的件数的乘积一定,总是6 000.
(3)xy=6 000,y与x成反比例关系.

(1) 这批零件共有多少件?
(2) 加工的天数是怎样随着每天加工的件数的变化而变化的?
(3) 用 $ y $ 表示加工的天数,用 $ x $ 表示每天加工的件数,用式子表示 $ y $ 与 $ x $ 的关系。$ y $ 与 $ x $ 成什么比例关系?
(1)100×60=6 000(件).答:这批零件共有6 000件.
(2)加工的天数随着每天加工的件数的变大而变小,而且加工的天数与每天加工的件数的乘积一定,总是6 000.
(3)xy=6 000,y与x成反比例关系.
答案:
(1)100×60=6 000(件).答:这批零件共有6 000件.
(2)加工的天数随着每天加工的件数的变大而变小,而且加工的天数与每天加工的件数的乘积一定,总是6 000.
(3)xy=6 000,y与x成反比例关系.
(1)100×60=6 000(件).答:这批零件共有6 000件.
(2)加工的天数随着每天加工的件数的变大而变小,而且加工的天数与每天加工的件数的乘积一定,总是6 000.
(3)xy=6 000,y与x成反比例关系.
8. 如图,自行车每节链条的长度为 $ 2.5 $ cm,交叉重叠部分的圆的直径为 $ 0.8 $ cm。
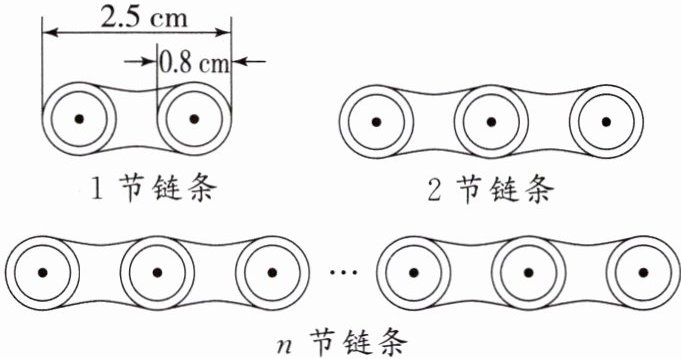
(1) $ 4 $ 节链条拉直后长度为
(2) $ n $ 节链条拉直后长度为
(3) 如果一辆自行车的链条由 $ 60 $ 节这样的链条首尾环形相连组成,那么该自行车链条环的长度为多少?

(1) $ 4 $ 节链条拉直后长度为
7.6
cm;(2) $ n $ 节链条拉直后长度为
(1.7n+0.8)
cm;(3) 如果一辆自行车的链条由 $ 60 $ 节这样的链条首尾环形相连组成,那么该自行车链条环的长度为多少?
因为自行车上的链条为环形,首尾环形相连,所以展直的长度应减1个0.8,故该自行车链条环的长度为1.7×60+0.8-0.8=102(cm)。
答案:
(1)2.5-0.8=1.7(cm).根据图形可得出:2节链条拉直后长度为(1.7×2+0.8)cm,3节链条拉直后长度为(1.7×3+0.8)cm,4节链条拉直后长度为1.7×4+0.8=7.6(cm).故答案为:7.6
(2)由
(1)可得n节链条拉直后长度为(1.7n+0.8)cm.故答案为:(1.7n+0.8)
(3)因为自行车上的链条为环形,首尾环形相连,所以展直的长度应减1个0.8,故该自行车链条环的长度为1.7×60+0.8-0.8=102(cm).
(1)2.5-0.8=1.7(cm).根据图形可得出:2节链条拉直后长度为(1.7×2+0.8)cm,3节链条拉直后长度为(1.7×3+0.8)cm,4节链条拉直后长度为1.7×4+0.8=7.6(cm).故答案为:7.6
(2)由
(1)可得n节链条拉直后长度为(1.7n+0.8)cm.故答案为:(1.7n+0.8)
(3)因为自行车上的链条为环形,首尾环形相连,所以展直的长度应减1个0.8,故该自行车链条环的长度为1.7×60+0.8-0.8=102(cm).
查看更多完整答案,请扫码查看


