《2025年新坐标同步练习七年级数学上册人教版青海专用》

12. 观察以下等式：
第 1 个等式：$ \frac{1}{2} + \frac{1}{1 × 2} = 1 $,第 2 个等式：$ \frac{1}{3} + \frac{1}{2 × 3} = \frac{1}{2} $,第 3 个等式：$ \frac{1}{4} + \frac{1}{3 × 4} = \frac{1}{3} $,第 4 个等式：$ \frac{1}{5} + \frac{1}{4 × 5} = \frac{1}{4} $,第 5 个等式：$ \frac{1}{6} + \frac{1}{5 × 6} = \frac{1}{5} $,……
按照以上规律解决下列问题：
(1)写出第 6 个等式：$\frac{1}{7}+\frac{1}{6×7}=\frac{1}{6}$；
(2)写出你猜想的第 $ n $ 个等式：$\frac{1}{n+1}+\frac{1}{n(n+1)}=\frac{1}{n}$(用含 $ n $ 的式子表示)。

答案：
(1)$\frac{1}{7}+\frac{1}{6×7}=\frac{1}{6}$
(2)$\frac{1}{n+1}+\frac{1}{n(n+1)}=\frac{1}{n}$

13. 新定义：若任意两数 $ a,b $,按规定 $ W = 7a - b $,通过运算得到一个新数 $ W $,则称所得新数 $ W $ 是数 $ a,b $ 的“快乐学习数”。
(1)若 $ a = 1,b = -2 $,求数 $ a,b $ 的“快乐学习数”$ W $；
(2)若 $ b = 5 $,数 $ a,b $ 的“快乐学习数”$ W $ 为 16,求 $ a $ 的值。

答案： 解:
(1)因为a=1,b=-2,
所以W=7a-b=7-(-2)=7+2=9.
所以数a,b的"快乐学习数"W为9.
(2)因为b=5,W=16,
所以16=7a-5,所以a=3.

14. 小丽在用等长的木棒设计图案,她先用 8 根木棒摆成图案①,再按图案①的个数逐次增加 1 的规律拼成图中的图案②和图案③。

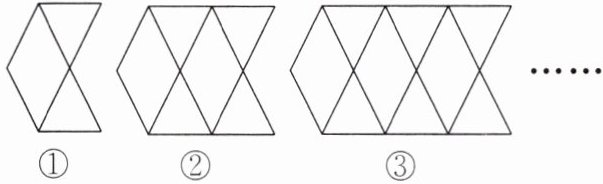
(1)她在摆图案⑤时,用了多少根木棒？
(2)请你帮她用含 $ n $ 的代数式表示图案 $\stackrel{n}{}$ 所需木棒的根数；
(3)如果要摆出图案 $\stackrel{50}{}$,所需木棒的根数是多少？

答案： 解:
(1)图案①中有8根木棒,
图案②中有14根木棒,
图案③中有20根木棒,
图案④中有26根木棒,
故图案⑤中有32根木棒.
所以她在摆图案⑤时,用了32根木棒.
(2)由
(1),得
8=2+6×1,
14=2+6×2,
20=2+6×3,
26=2+6×4,
32=2+6×5,
……,
所以图案n所需木棒的根数是(2+6n).
(3)当n=50时,2+6n=2+6×50=302(根),
所以要摆出图案50,所需木棒的根数是302.