《2025年新学案暑假作业七年级数学》

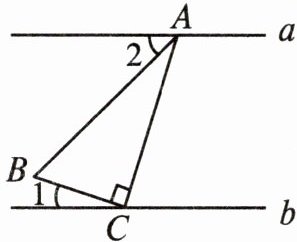
6. 如图,$a// b$,将一个含$30^{\circ }$角($∠BAC= 30^{\circ }$)的三角尺按图中方式放置,其中顶点$A和C分别落在直线a和b$上。若$∠1= 20^{\circ }$,则$∠2$的度数是(C)

A.$20^{\circ }$
B.$30^{\circ }$
C.$40^{\circ }$
D.$50^{\circ }$

答案： C [因为 $ a // b $，
所以 $ \angle 1 + \angle BCA + \angle 2 + \angle BAC = 180 ^ { \circ } $.
因为 $ \angle BAC = 30 ^ { \circ } $，$ \angle BCA = 90 ^ { \circ } $，$ \angle 1 = 20 ^ { \circ } $，
所以 $ \angle 2 = 40 ^ { \circ } $. 故选 C.]

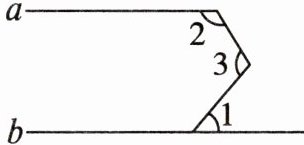
7. 如图,$a// b$,$∠1= 50^{\circ }$,$∠2= 120^{\circ }$,则$∠3$的度数是(B)

A.$100^{\circ }$
B.$110^{\circ }$
C.$120^{\circ }$
D.$130^{\circ }$

答案： B

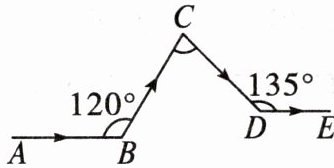
8. 如图,某人某次行车过程中共拐了三次弯,最后行车路线$DE与开始的路线AB$是平行的,则$∠C$的度数是(A)

A.$75^{\circ }$
B.$120^{\circ }$
C.$135^{\circ }$
D.无法确定

答案： A

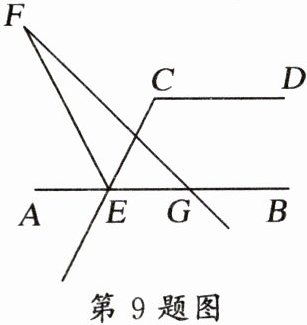
9. 如图,$AB// CD$,$∠DCE= 118^{\circ }$,$∠AEC的平分线EF与GF相交于点F$,$∠BGF= 132^{\circ }$,则$∠F$的度数是______11°。

答案： $ 11 ^ { \circ } $

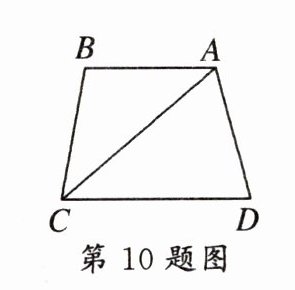
10. 如图,$AB// CD$,$∠D= 80^{\circ }$,$∠CAD:∠BAC= 3:2$,则$∠CAD$的度数是$60^{\circ }$,$∠ACD$的度数是$40^{\circ }$。

答案： $ 60 ^ { \circ } $ $ 40 ^ { \circ } $

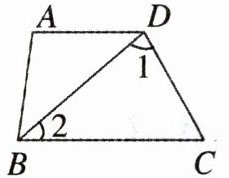
11. 如图,$AD// BC$,$∠1= 78^{\circ }$,$∠2= 40^{\circ }$,则$∠ADC$的度数是$118^{\circ }$。

答案： $ 118 ^ { \circ } $

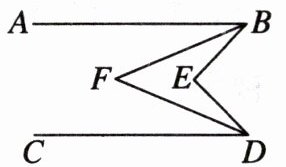
12. 如图,$AB// CD$,$BF平分∠ABE$,$DF平分∠CDE$,$∠BED= 92^{\circ }$,则$∠BFD$的度数是______$46^{\circ }$。

答案： $ 46 ^ { \circ } $

13. 如图,$AB// CD$。分别探讨下面四个图形中$∠APC与∠PAB$,$∠PCD$的关系。请你从所得到的关系中任选一个加以证明。

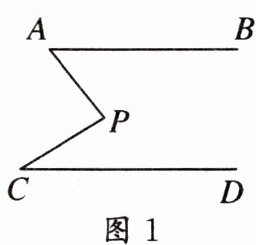
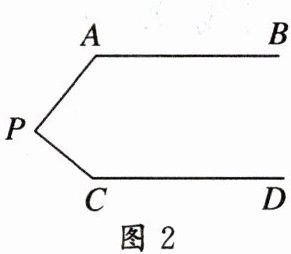
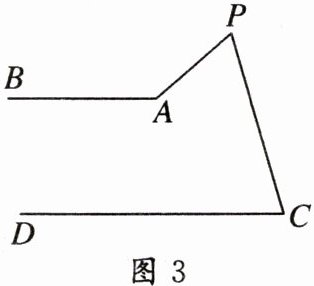
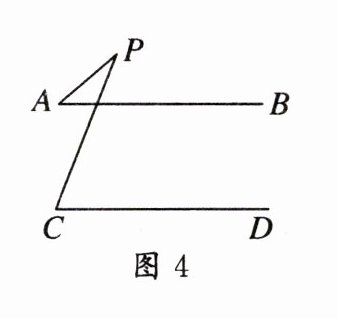
答案：
解：说明关系可参考下图.

(1) $ \angle APC = \angle PAB + \angle PCD $.
证明：如图 1，过点 $ P $ 作 $ PF // AB $，
则 $ AB // CD // PF $，
所以 $ \angle APF = \angle PAB $，$ \angle CPF = \angle PCD $.
所以 $ \angle APC = \angle PAB + \angle PCD $.
(2) $ \angle APC + \angle PAB + \angle PCD = 360 ^ { \circ } $.
(3) $ \angle APC = \angle PAB - \angle PCD $.
(4) $ \angle APC = \angle PCD - \angle PAB $.