2025年新学案暑假作业七年级数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年新学案暑假作业七年级数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
5. 数学课上,同学们在练习“过点$B作线段AC$所在直线的垂线段”时,有一部分同学画出下列四种图形,请你数一数,其中错误的个数为(
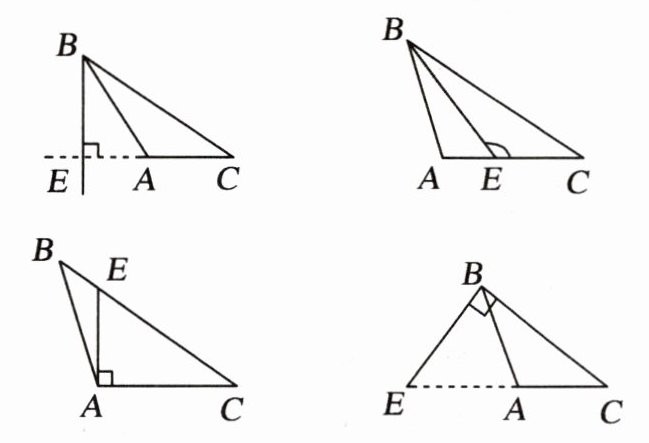
A.$1$
B.$2$
C.$3$
D.$4$
D
)
A.$1$
B.$2$
C.$3$
D.$4$
答案:
D
6. 已知直线$AB$,$CD相交于点O$,$OE$,$OF$,$OG分别平分∠AOC$,$∠BOC$,$∠AOD$,则下列说法中正确的是(
A.$OE$,$OF$在同一条直线上
B.$OE$,$OG$在同一条直线上
C.$OG⊥OF$
D.$OE⊥OF$
D
)A.$OE$,$OF$在同一条直线上
B.$OE$,$OG$在同一条直线上
C.$OG⊥OF$
D.$OE⊥OF$
答案:
D
7. 如图所示,直线$AB$,$CD相交于点O$,$OE⊥CD$,$∠BOE= 54^{\circ}$,则$∠AOC$等于(

A.$54^{\circ}$
B.$46^{\circ}$
C.$36^{\circ}$
D.$26^{\circ}$
C
)
A.$54^{\circ}$
B.$46^{\circ}$
C.$36^{\circ}$
D.$26^{\circ}$
答案:
C
8. 关于题目所给的图形,现有下列结论:①$MB<MC$;②$MA>AC$;③$MB<AC$。其中正确的结论有(
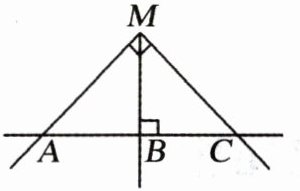
A.$0$个
B.$1$个
C.$2$个
D.$3$个
C
)
A.$0$个
B.$1$个
C.$2$个
D.$3$个
答案:
C [因为 $ MB \perp AC $,所以 $ MB < MC $,$ MB < MA $,所以①正确.因为 $ MA \perp MC $,所以 $ MA < AC $,所以②错误.因为 $ MA > MB $,$ MA < AC $,所以 $ MB < AC $,所以③正确.综上所述,正确的结论有 2 个,故选 C.]
9. 如图,$AB⊥CD$,垂足为$O$,$EF经过点O$,$∠2= 2∠1$,那么$∠2= $

$60^{\circ}$
,$∠3= $$30^{\circ}$
。
答案:
$ 60^{\circ} $ $ 30^{\circ} $
10. 如图,直线$AB$,$CD相交于点O$。若$∠EOC:∠EOD= 4:5$,$OA平分∠EOC$,则$∠BOE= $
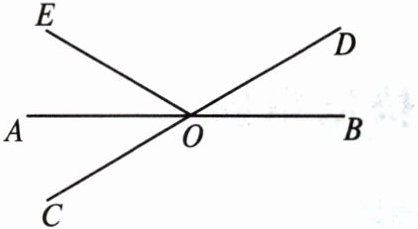
$140^{\circ}$
。
答案:
$ 140^{\circ} $ [因为 $ \angle EOC : \angle EOD = 4 : 5 $,所以设 $ \angle EOC = 4x $,$ \angle EOD = 5x $.因为 $ \angle EOC + \angle EOD = 180^{\circ} $,所以 $ 4x + 5x = 180^{\circ} $,解得 $ x = 20^{\circ} $.所以 $ \angle EOC = 80^{\circ} $,$ \angle EOD = 100^{\circ} $.因为 $ OA $ 平分 $ \angle EOC $,所以 $ \angle COA = \angle AOE = 40^{\circ} $.所以 $ \angle BOE = 180^{\circ} - \angle AOE = 140^{\circ} $.故答案为 $ 140^{\circ} $.]
11. 如图,把一张报纸的一角折过去,使点$A落在点E$处,$BC$为折痕。若$BD是∠EBM$的平分线,则$∠CBD= $
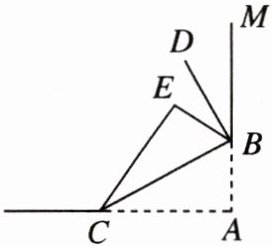
$90^{\circ}$
。
答案:
$ 90^{\circ} $ [因为把点 $ A $ 折过去落在点 $ E $ 处,所以 $ \angle ABC = \angle CBE = \frac{1}{2} \angle ABE $.因为 $ BD $ 是 $ \angle EBM $ 的平分线,所以 $ \angle EBD = \angle DBM = \frac{1}{2} \angle EBM $.又因为 $ \angle ABE + \angle EBM = 180^{\circ} $,所以 $ \angle CBD = \angle CBE + \angle EBD = \frac{1}{2} \angle ABE + \frac{1}{2} \angle EBM = \frac{1}{2} (\angle ABE + \angle EBM) = \frac{1}{2} × 180^{\circ} = 90^{\circ} $.故答案为 $ 90^{\circ} $.]
12. (1)(如图1,两条水平的直线被一条直线所截,同位角有
(2)(如图2,三条水平的直线被一条直线所截,同位角有
(3)根据(1)(2)的结果推测:n(n为大于1的整数)条水平直线被一条直线所截,同位角有
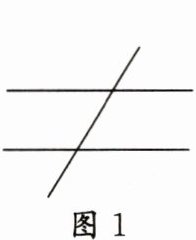

4
对,内错角有2
对,同旁内角有2
对;(2)(如图2,三条水平的直线被一条直线所截,同位角有
12
对,内错角有6
对,同旁内角有6
对;(3)根据(1)(2)的结果推测:n(n为大于1的整数)条水平直线被一条直线所截,同位角有
2n(n - 1)
对,内错角有n(n - 1)
对,同旁内角有n(n - 1)
对。(用含n的式子表示)

答案:
(1) 4 2 2
(2) 12 6 6
(3) $ 2n(n - 1) $ $ n(n - 1) $ $ n(n - 1) $
(1) 4 2 2
(2) 12 6 6
(3) $ 2n(n - 1) $ $ n(n - 1) $ $ n(n - 1) $
查看更多完整答案,请扫码查看


