2025年新学案暑假作业七年级数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年新学案暑假作业七年级数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
6. 在同一平面内,过一点作已知直线的平行线(
A.能且只能作一条
B.不能作出
C.能作两条
D.不能作出或能且只能作一条
D
)A.能且只能作一条
B.不能作出
C.能作两条
D.不能作出或能且只能作一条
答案:
D
7. 一辆汽车在笔直的公路上行驶,两次拐弯后仍与原来的行驶方向相同。该汽车两次拐弯的方向和角度可能是(
A.第一次向右拐 $ 40^\circ $,第二次向左拐 $ 140^\circ $
B.第一次向左拐 $ 40^\circ $,第二次向右拐 $ 40^\circ $
C.第一次向左拐 $ 40^\circ $,第二次向右拐 $ 140^\circ $
D.第一次向右拐 $ 40^\circ $,第二次向右拐 $ 40^\circ $
B
)A.第一次向右拐 $ 40^\circ $,第二次向左拐 $ 140^\circ $
B.第一次向左拐 $ 40^\circ $,第二次向右拐 $ 40^\circ $
C.第一次向左拐 $ 40^\circ $,第二次向右拐 $ 140^\circ $
D.第一次向右拐 $ 40^\circ $,第二次向右拐 $ 40^\circ $
答案:
B
8. 若同一平面内的四条直线 $ a $,$ b $,$ c $,$ d $ 满足 $ a \perp b $,$ b \perp c $,$ c \perp d $,则下列结论中正确的是(
A.$ a // d $
B.$ b \perp d $
C.$ a \perp d $
D.$ b // c $
C
)A.$ a // d $
B.$ b \perp d $
C.$ a \perp d $
D.$ b // c $
答案:
C
9. 下图给出了“过直线外一点 $ P $ 作已知直线 $ l $ 的平行线”的方法,其依据是

同位角相等,两直线平行
。
答案:
同位角相等,两直线平行
10. 如图是一条街道的两个拐角,$ \angle ABC $ 与 $ \angle BCD $ 均为 $ 140^\circ $,则街道 $ AB $ 与 $ CD $ 的位置关系是 ______
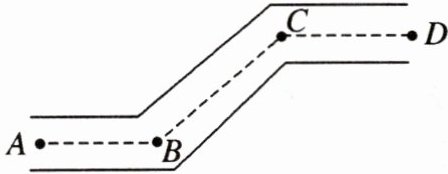
平行
,这是因为 ______内错角相等,两直线平行
。
答案:
平行 内错角相等,两直线平行
11. 如图,$ \angle A = 70^\circ $,直线 $ OD $ 与 $ AB $ 相交,$ \angle BOD = 82^\circ $。要使 $ OD // AC $,直线 $ OD $ 需绕点 $ O $ 按逆时针方向旋转至少 ______

12
度。
答案:
12
12. 将一副三角尺按如图所示的方式叠放在一起,其中点 $ C $,$ D $ 重合。固定三角尺 $ ABC $,旋转三角尺 $ AED $(其中点 $ A $ 的位置始终不变),当 $ \angle CAD = $ ______ 时,$ DE // AC $。
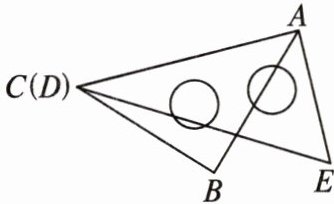

答案:
$30^{\circ}$或$150^{\circ}$ [①如图1,当$\angle CAD = \angle D = 30^{\circ}$时,$DE // AC$.
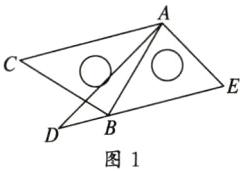
②如图2,当$\angle EAC = \angle E = 60^{\circ}$时,$DE // AC$,所以$\angle CAD = 60^{\circ} + 90^{\circ} = 150^{\circ}$.
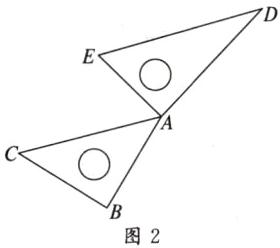
故答案为$30^{\circ}$或$150^{\circ}$.
$30^{\circ}$或$150^{\circ}$ [①如图1,当$\angle CAD = \angle D = 30^{\circ}$时,$DE // AC$.

②如图2,当$\angle EAC = \angle E = 60^{\circ}$时,$DE // AC$,所以$\angle CAD = 60^{\circ} + 90^{\circ} = 150^{\circ}$.

故答案为$30^{\circ}$或$150^{\circ}$.
13. 将一副三角尺拼成如图所示的图形,过点 $ C $ 作 $ CF $ 平分 $ \angle DCE $,交 $ DE $ 于点 $ F $。

(1)求证:$ CF // AB $;
(2)求 $ \angle DFC $ 的度数。

(1)求证:$ CF // AB $;
(2)求 $ \angle DFC $ 的度数。
答案:
(1) 证明:因为$CF$平分$\angle DCE$,所以$\angle DCF = \angle ECF = \frac{1}{2}\angle DCE$. 因为$\angle DCE = 90^{\circ}$,所以$\angle DCF = 45^{\circ}$. 又因为$\angle BAC = 45^{\circ}$,所以$\angle BAC = \angle DCF$. 所以$AB // CF$.
(2) 解:因为$\angle D = 30^{\circ}$,$\angle DCF = 45^{\circ}$,所以$\angle DFC = 180^{\circ} - 30^{\circ} - 45^{\circ} = 105^{\circ}$.
(1) 证明:因为$CF$平分$\angle DCE$,所以$\angle DCF = \angle ECF = \frac{1}{2}\angle DCE$. 因为$\angle DCE = 90^{\circ}$,所以$\angle DCF = 45^{\circ}$. 又因为$\angle BAC = 45^{\circ}$,所以$\angle BAC = \angle DCF$. 所以$AB // CF$.
(2) 解:因为$\angle D = 30^{\circ}$,$\angle DCF = 45^{\circ}$,所以$\angle DFC = 180^{\circ} - 30^{\circ} - 45^{\circ} = 105^{\circ}$.
查看更多完整答案,请扫码查看


