2025年暑假作业贵州人民出版社八年级物理人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假作业贵州人民出版社八年级物理人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第65页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
10. 某挖掘机在 6s 内将装满铲斗的质量为 0.75t 的泥土提起并送到 10m 外的岸边,挖掘深度$H = 2m$(如图乙所示),已知发动机的总功率是 20kW,(g 取 10N/kg)则(
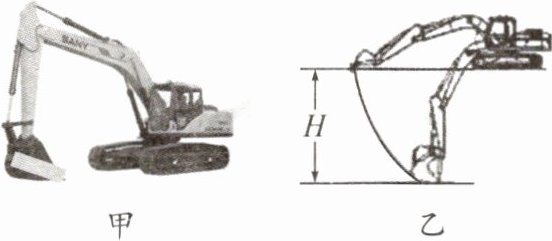
A.挖掘机每挖一次泥土并水平移送到岸边,挖掘机对泥土做功为$7.5×10^{4}J$
B.挖掘机每挖一次泥土并水平移送到岸边,挖掘机对泥土做功为$9×10^{4}J$
C.挖泥过程中挖掘机的机械效率为 12.5%
D.挖泥过程中挖掘机的额外功为$0.3×10^{4}J$
C
)
A.挖掘机每挖一次泥土并水平移送到岸边,挖掘机对泥土做功为$7.5×10^{4}J$
B.挖掘机每挖一次泥土并水平移送到岸边,挖掘机对泥土做功为$9×10^{4}J$
C.挖泥过程中挖掘机的机械效率为 12.5%
D.挖泥过程中挖掘机的额外功为$0.3×10^{4}J$
答案:
C
11. 筒车是一种以水流作动力来取水的机械,简易图如图甲所示。若接水槽离取水处高 3m,水轮上有 12 个取水筒,一个取水筒每次可取水 5kg,筒车旋转一周所用时间为 60s。水流冲击的动能转化为筒车转动的动能和筒内水的
重力势
能。若水流冲击筒车的功率为 50W,则筒车匀速旋转一周取水的机械效率是60
%。提升重物还可以使用滑轮组,如图乙所示,工人用滑轮组匀速提升重 800N 的货物,所用的拉力 F 为 500N,货物在 50s 内匀速上升 5m,拉力做功的功率是100
W,滑轮组的机械效率是80
%。(g 取 10N/kg)
答案:
重力势 60 100 80
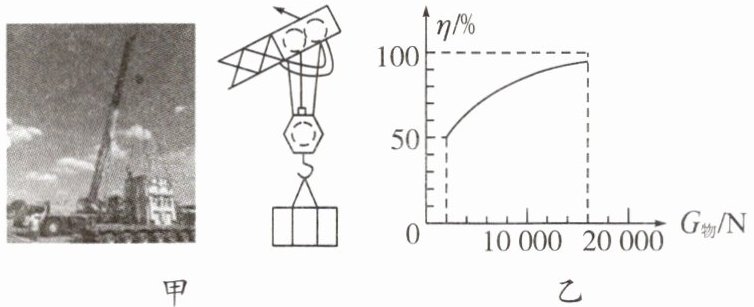
12. 建筑工地上,施工人员用起重机吊臂上的滑轮组吊起建筑材料,可简化成如图甲所示的滑轮组。每个滑轮等重,不计绳重及摩擦,物重从$G_{物}= 2000N$开始逐渐增加,直到绳子被拉断,每次以 0.15m/s 匀速拉动绳子将物体提升同样的高度。图乙记录了在此过程中滑轮组的机械效率随物体重力的增加而变化的图像。求:
(1)每个滑轮所受重力为
(2)绳子能承受的最大拉力为
(3)当滑轮组的机械效率为 80%时,起重机的功率为

(1)每个滑轮所受重力为
2000N
;(2)绳子能承受的最大拉力为
6000N
;(3)当滑轮组的机械效率为 80%时,起重机的功率为
500W
。
答案:
解:
(1)由图甲可知,承担物重的绳子段数$n =3$。不计绳重及摩擦,滑轮组的机械效率$\eta=\frac{W_{有}}{W_{总}}=\frac{G_{物}h}{(G_{物}+G_{动})h}=\frac{G_{物}}{G_{物}+G_{动}}$。由图乙可知,当$G_{物}=2000N$时,$\eta = 50\%$,则$50\%=\frac{2000N}{2000N+G_{动}}$,解得$G_{动}=2000N$。
即每个滑轮所受重力为2000N。
(2)由图乙可知,绳子能承受的最大物重$G_{max}=16000N$。不计绳重及摩擦,绳子能承受的最大拉力$F_{max}=\frac{G_{max}+G_{动}}{n}=\frac{16000N + 2000N}{3}=6000N$。
(3)当$\eta = 80\%$时,$\eta=\frac{G_{物}}{G_{物}+G_{动}}$,即$80\%=\frac{G_{物}}{G_{物}+2000N}$,解得$G_{物}=8000N$。此时拉力$F=\frac{G_{物}+G_{动}}{n}=\frac{8000N+2000N}{3}=\frac{10000}{3}N$。绳子自由端速度$v = 0.15m/s$,起重机的功率$P=Fv=\frac{10000}{3}N×0.15m/s = 500W$。
(1)由图甲可知,承担物重的绳子段数$n =3$。不计绳重及摩擦,滑轮组的机械效率$\eta=\frac{W_{有}}{W_{总}}=\frac{G_{物}h}{(G_{物}+G_{动})h}=\frac{G_{物}}{G_{物}+G_{动}}$。由图乙可知,当$G_{物}=2000N$时,$\eta = 50\%$,则$50\%=\frac{2000N}{2000N+G_{动}}$,解得$G_{动}=2000N$。
即每个滑轮所受重力为2000N。
(2)由图乙可知,绳子能承受的最大物重$G_{max}=16000N$。不计绳重及摩擦,绳子能承受的最大拉力$F_{max}=\frac{G_{max}+G_{动}}{n}=\frac{16000N + 2000N}{3}=6000N$。
(3)当$\eta = 80\%$时,$\eta=\frac{G_{物}}{G_{物}+G_{动}}$,即$80\%=\frac{G_{物}}{G_{物}+2000N}$,解得$G_{物}=8000N$。此时拉力$F=\frac{G_{物}+G_{动}}{n}=\frac{8000N+2000N}{3}=\frac{10000}{3}N$。绳子自由端速度$v = 0.15m/s$,起重机的功率$P=Fv=\frac{10000}{3}N×0.15m/s = 500W$。
查看更多完整答案,请扫码查看


