1. 已知$\triangle ABC\cong\triangle DEF$,$\angle A = 50^{\circ}$,$\angle C = 30^{\circ}$,则$\angle E$的度数是(
A.$30^{\circ}$
B.$50^{\circ}$
C.$60^{\circ}$
D.$100^{\circ}$
D
)A.$30^{\circ}$
B.$50^{\circ}$
C.$60^{\circ}$
D.$100^{\circ}$
答案:
1.D
2. 有下列命题:①全等三角形的对应角相等;②周长相等的两个三角形全等;③全等三角形对应边上的中线相等;④有两条边和一个角对应相等的两个三角形全等.其中正确的命题有(
A.1 个
B.2 个
C.3 个
D.4 个
B
)A.1 个
B.2 个
C.3 个
D.4 个
答案:
2.B
3. 如图,点$B$,$F$,$C$,$E$共线,$\angle B = \angle E$,$BF = EC$,添加一个条件,不能判定$\triangle ABC\cong\triangle DEF$的是(
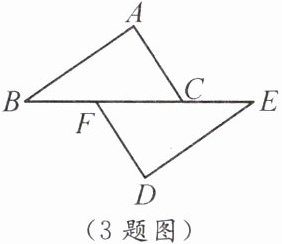
A.$AB = DE$
B.$\angle A = \angle D$
C.$AC = DF$
D.$AC// FD$
C
)
A.$AB = DE$
B.$\angle A = \angle D$
C.$AC = DF$
D.$AC// FD$
答案:
3.C
4. 如图,在$\triangle ABC$中,$E$为$AC$的中点,$CN// AB$,$NE$的延长线交$AB$于点$M$.若$MB = 6$,$CN = 2$,则$AB$的长为(

A.7
B.8
C.9
D.10
B
)
A.7
B.8
C.9
D.10
答案:
4.B
5. 如图,$\triangle ABC\cong\triangle AEF$.有下列结论:①$AC = AE$;②$\angle FAB = \angle EAB$;③$EF = BC$;④$\angle EAB = \angle FAC$.其中正确的有(
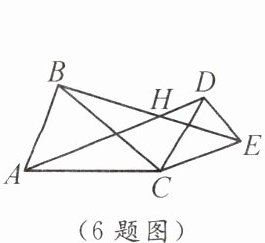
A.1 个
B.2 个
C.3 个
D.4 个
B
)
A.1 个
B.2 个
C.3 个
D.4 个

答案:
5.B
6. 如图,$CA = CB$,$CD = CE$,$\angle ACB = \angle DCE = 40^{\circ}$,连接$AD$,$BE$交于点$H$,则$\angle AHE$的度数为(
A.$160^{\circ}$
B.$140^{\circ}$
C.$130^{\circ}$
D.$110^{\circ}$
B
)A.$160^{\circ}$
B.$140^{\circ}$
C.$130^{\circ}$
D.$110^{\circ}$
答案:
6.B
7. 如图,已知$\triangle ABC$与$\triangle DFE$,$B$,$E$,$C$,$D$四点在同一条直线上,其中$AB = DF$,$BC = FE$,$AC = DE$,则$\angle ACB$等于(

A.$\angle EFD$
B.$\angle ABC$
C.$2\angle D$
D.$\frac{1}{2}\angle AFE$
D
)
A.$\angle EFD$
B.$\angle ABC$
C.$2\angle D$
D.$\frac{1}{2}\angle AFE$
答案:
7.D
8. 如图,$AD$是$\triangle ABC$的中线,点$E$,$F$分别在$AB$,$AC$上,且$DE\perp DF$,则$BE + CF$与$EF$的大小关系是(

A.$BE + CF>EF$
B.$BE + CF = EF$
C.$BE + CF<EF$
D.无法确定
A
)
A.$BE + CF>EF$
B.$BE + CF = EF$
C.$BE + CF<EF$
D.无法确定
答案:
8.A
9. 如图,$AC = AD$,$\angle 1 = \angle 2$,要使$\triangle ABC\cong\triangle AED$,应添加的条件是
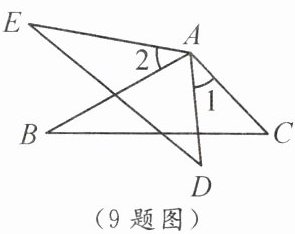
$\angle B = \angle E$
(写出一个条件即可).
答案:
9.$\angle B = \angle E$
10. 如图,在三角形纸片$ABC$中,$AB = 9\ cm$,$BC = 7\ cm$,$AC = 6\ cm$,沿过点$B$的直线折叠这张三角形纸片使顶点$C$落在边$AB$上的点$E$处,折痕为$BD$,则$\triangle AED$的周长为

8
$cm$.
答案:
10.8
查看更多完整答案,请扫码查看


