14. 已知 $(a^{m + 1}b^{n + 2}) ÷ (a^{n}b^{4 - m}) = a^{3}b^{2}$,则 $n^{m}$ 的值是
1
.
答案:
14.1
15. 计算:
(1) $(-x)^{5} ÷ (-x)^{2} \cdot x^{2}$;
(2) $[a^{3} \cdot a^{5} + (3a^{4})^{2}] ÷ a^{2}$;
(3) $3a^{2}(a^{3}b^{2} - 2a) - 4a(-a^{2}b)^{2}$.
(1) $(-x)^{5} ÷ (-x)^{2} \cdot x^{2}$;
(2) $[a^{3} \cdot a^{5} + (3a^{4})^{2}] ÷ a^{2}$;
(3) $3a^{2}(a^{3}b^{2} - 2a) - 4a(-a^{2}b)^{2}$.
答案:
15.
(1)解:原式$=(-x)^{3}\cdot x^{2}=-x^{5}.$
(2)解:原式$=(a^{8}+9a^{8})÷ a^{2}=10a^{6}.$
(3)解:原式$=3a^{5}b^{2}-6a^{3}-4a^{5}b^{2}=-a^{5}b^{2}-6a^{3}.$
(1)解:原式$=(-x)^{3}\cdot x^{2}=-x^{5}.$
(2)解:原式$=(a^{8}+9a^{8})÷ a^{2}=10a^{6}.$
(3)解:原式$=3a^{5}b^{2}-6a^{3}-4a^{5}b^{2}=-a^{5}b^{2}-6a^{3}.$
16. 解答下列各题:
(1) 先化简,再求值:$[x(x^{2}y^{2} + xy) - y(x^{2} - x^{3}y)] ÷ (3x^{2}y)$,其中 $\vert x + 2 \vert + (y - 3)^{2} = 0$.
(2) 已知 $3x - y = 2$,求 $[(x^{2} + y^{2}) - (x + y)(x - y) + 2y(3x - 2y)] ÷ (4y)$ 的值.
(3) 先化简,再求值:$x(7x + 1) - 3(x - 1)(x - 2) + 2$,其中 $x$ 满足 $(a^{2x + 1})^{2} = a^{6x} ÷ a^{8}$.
(4) 若 $x^{2} + 3x + 1 = 0$,求代数式 $x(x + 1)(x + 2)(x + 3)$ 的值.
(1) 先化简,再求值:$[x(x^{2}y^{2} + xy) - y(x^{2} - x^{3}y)] ÷ (3x^{2}y)$,其中 $\vert x + 2 \vert + (y - 3)^{2} = 0$.
(2) 已知 $3x - y = 2$,求 $[(x^{2} + y^{2}) - (x + y)(x - y) + 2y(3x - 2y)] ÷ (4y)$ 的值.
(3) 先化简,再求值:$x(7x + 1) - 3(x - 1)(x - 2) + 2$,其中 $x$ 满足 $(a^{2x + 1})^{2} = a^{6x} ÷ a^{8}$.
(4) 若 $x^{2} + 3x + 1 = 0$,求代数式 $x(x + 1)(x + 2)(x + 3)$ 的值.
答案:
16.
(1)解:原式$=(x^{3}y^{2}+x^{2}y-x^{2}y+x^{3}y^{2})÷(3x^{2}y)=$
$(2x^{3}y^{2})÷(3x^{2}y)=\frac{2}{3}xy.\because \left$|$x + 2\right$|$\geq0,(y - 3)^{2}\geq0,\therefore x +$
2=0,y - 3=0,解得$x=-2,y=3,\therefore$原式$=\frac{2}{3}×(-2)×3=$
-4.
(2)解:原式$=[x^{2}+y^{2}-(x^{2}-y^{2})+6xy - 4y^{2}]÷(4y)=$
$(6xy - 2y^{2})÷(4y)=\frac{1}{2}(3x - y).$当3x - y=2时,原式=
$\frac{1}{2}×2=1.$
(3)解:原式$=7x^{2}+x - 3(x^{2}-3x + 2)+2=7x^{2}+x - 3x^{2}+$
$9x - 6 + 2=4x^{2}+10x - 4.\because (a^{2x + 1})^{2}=a^{6x}÷ a^{8},\therefore a^{4x + 2}=$
$a^{6x - 8},\therefore4x + 2=6x - 8,$解得x=5.当x=5时,原式=4×
$5^{2}+10×5 - 4=146.$
(4)解:原式$=[x(x + 3)]\cdot[(x + 1)(x + 2)]=(x^{2}+$
$3x)(x^{2}+3x + 2).\because x^{2}+3x + 1=0,\therefore x^{2}+3x=-1,\therefore$原
式=(-1)×(-1 + 2)=-1.
(1)解:原式$=(x^{3}y^{2}+x^{2}y-x^{2}y+x^{3}y^{2})÷(3x^{2}y)=$
$(2x^{3}y^{2})÷(3x^{2}y)=\frac{2}{3}xy.\because \left$|$x + 2\right$|$\geq0,(y - 3)^{2}\geq0,\therefore x +$
2=0,y - 3=0,解得$x=-2,y=3,\therefore$原式$=\frac{2}{3}×(-2)×3=$
-4.
(2)解:原式$=[x^{2}+y^{2}-(x^{2}-y^{2})+6xy - 4y^{2}]÷(4y)=$
$(6xy - 2y^{2})÷(4y)=\frac{1}{2}(3x - y).$当3x - y=2时,原式=
$\frac{1}{2}×2=1.$
(3)解:原式$=7x^{2}+x - 3(x^{2}-3x + 2)+2=7x^{2}+x - 3x^{2}+$
$9x - 6 + 2=4x^{2}+10x - 4.\because (a^{2x + 1})^{2}=a^{6x}÷ a^{8},\therefore a^{4x + 2}=$
$a^{6x - 8},\therefore4x + 2=6x - 8,$解得x=5.当x=5时,原式=4×
$5^{2}+10×5 - 4=146.$
(4)解:原式$=[x(x + 3)]\cdot[(x + 1)(x + 2)]=(x^{2}+$
$3x)(x^{2}+3x + 2).\because x^{2}+3x + 1=0,\therefore x^{2}+3x=-1,\therefore$原
式=(-1)×(-1 + 2)=-1.
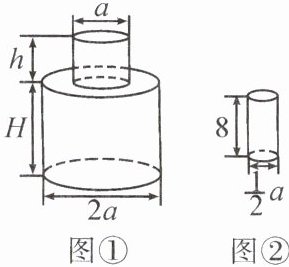
17. 如图,图①的瓶子中盛满水,如果将这个瓶子中的水全部倒入图②的小杯子中,那么你知道一共需要多少个这样的杯子吗?

答案:
17.解:$[\pi(\frac{1}{2}a)^{2}h+\pi(\frac{1}{2}×2a)^{2}H]÷[\pi(\frac{1}{2}×\frac{1}{2}a)^{2}×8]=$
$(\frac{1}{4}\pi a^{2}h+\pi a^{2}H)÷(\frac{1}{2}\pi a^{2})=\frac{1}{2}h + 2H.$答:一共需要
$(\frac{1}{2}h + 2H)$个小杯子。
$(\frac{1}{4}\pi a^{2}h+\pi a^{2}H)÷(\frac{1}{2}\pi a^{2})=\frac{1}{2}h + 2H.$答:一共需要
$(\frac{1}{2}h + 2H)$个小杯子。
查看更多完整答案,请扫码查看


