《2025年超越训练八年级数学上册人教版四川专版》

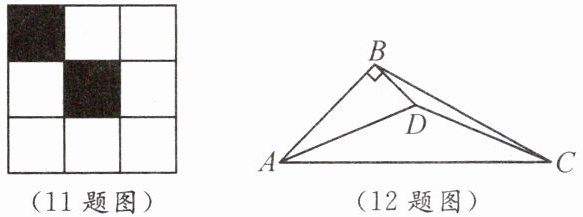
11. 如图,在 $ 3 × 3 $ 的正方形网格中,已有两个小正方形被涂黑,再将图中其余小正方形涂黑一个,使被涂黑的部分构成一个轴对称图形,有5种涂法.

答案： 11.5

12. 如图,在 $ \triangle ABC $ 中,$ AD $ 平分 $ \angle BAC $,$ DB \perp AB $,$ DA = DC $.若 $ AB = 2 $,则 $ AC $ 的长为4.

答案： 12.4

13. 如图,在 $ \triangle ABC $ 中,$ AB = AC $,$ \angle A = 36^{\circ} $,$ BD $ 平分 $ \angle ABC $ 交 $ AC $ 于点 $ D $.若 $ BC = 2 $,则 $ AD $ 的长为2.

答案： 13.2

14. 如图,在 $ \triangle ABC $ 中,$ \angle BAC = 80^{\circ} $,$ AB $,$ AC $ 的垂直平分线分别交 $ BC $ 于点 $ D $,$ E $,连接 $ AD $,$ AE $,则 $ \angle DAE $ 的度数为20°.

答案： 14.20°

15. 如图,在 $ \triangle ABC $ 中,$ AB = AC $,$ BF = CD $,$ BD = CE $,则 $ \angle A $ 与 $ \angle FDE $ 的数量关系为2∠FDE+∠A=180°.

答案： 15.2∠FDE+∠A=180°

16. 如图,在 $ \triangle ABC $ 中,$ \angle C = 90^{\circ} $,$ AC = BC $,$ O $ 为 $ AB $ 的中点,过点 $ O $ 作 $ OM \perp ON $,分别交 $ AC $,$ BC $ 于点 $ M $,$ N $.若 $ CM = 4 $,$ CN = 2 $,则 $ \triangle ABC $ 的面积为18.

答案： 16.18

17. $ \triangle ABC $ 在平面直角坐标系中的位置如图所示.
(1) 画出与 $ \triangle ABC $ 关于 $ y $ 轴对称的 $ \triangle A_1B_1C_1 $,并写出点 $ B_1 $ 的坐标.
(2) 将 $ \triangle ABC $ 向右平移 8 个单位长度,画出平移后的 $ \triangle A_2B_2C_2 $,并写出点 $ B_2 $ 的坐标.
(3) $ \triangle A_1B_1C_1 $ 与 $ \triangle A_2B_2C_2 $ 有怎样的位置关系?

答案：
17.解:
(1)如图,△A₁B₁C₁即为所求;B₁(3,2).
(2)如图,△A₂B₂C₂即为所求;B₂(5,2).
(3)△A₁B₁C₁与△A₂B₂C₂关于直线x=4对称.
　　　　　　　　

18. 如图,在 $ \triangle ABC $ 中,$ \angle ACB = 90^{\circ} $,$ D $ 为 $ AB $ 上一点,$ O $ 为 $ AB $ 的中点,$ AC = BD = BC $,连接 $ CD $,过点 $ C $ 作 $ CE \perp CD $,且 $ CE = CD $,连接 $ DE $ 交 $ CB $ 于点 $ F $.求证:
(1) $ \triangle ACD \cong \triangle BDF $;
(2) $ CF = 2OD $.

答案：
18.证明:
(1)
∵∠ACB=90°，AC=BC，
∴∠A=∠B=45°.
∵CE⊥CD，CE=CD，
∴∠CDE=45°.
∵∠CDB=∠CDE+∠BDF=∠A+∠ACD，
∴45°+∠BDF=45°+∠ACD，
∴∠BDF=∠ACD.又AC=BD，
∴△ACD≌△BDF(ASA).
(2)如图，连接CO，过点D作DH⊥CF于点H.由
(1)，得△ACD≌△BDF，
∴DC=DF.
∵DH⊥CF，
∴CF=2HC.
∵BD=BC，
∴∠ODC=∠HCD.又∠COD=∠DHC，CD=DC，
∴△OCD≌△HDC(AAS)，
∴OD=HC，
∴CF=2OD.