12. 如图,在$\triangle ABC$中,$∠BAC = 70°$,$∠1 = ∠2$,则$∠ADC$的度数是
110°
.
答案:
12.110°
13. 如图,在$\triangle ABC$中,若$∠A = 40°$,$∠B = 72°$,$CE$平分$∠ACB$,$CD \perp AB$,垂足为$D$,$DF \perp CE$,垂足为$F$,则$∠CDF$的度数是
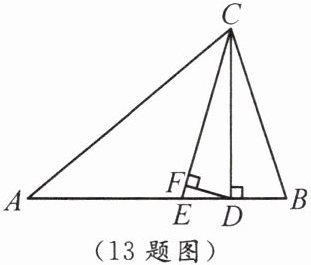
74°
.

答案:
13.74°
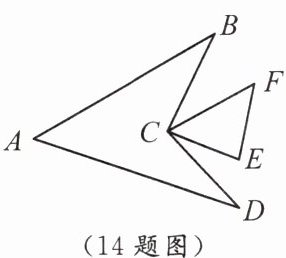
14. 如图,在$\triangle CEF$中,$∠E = 80°$,$∠F = 50°$,$AB // CF$,$AD // CE$,连接$BC$,$CD$,则$∠A$的度数是
50°
.
答案:
14.50°
15. 如图,在$\triangle ABC$中,$AD$是高,$AE$平分$∠BAC$交$BC$于点$E$,过点$E$作$EF \perp AC$,垂足为$F$.若$∠DAE = \alpha$,$∠AEF = \beta$,求$∠B$的度数(用含$\alpha$,$\beta$的代数式表示).


答案:
15.解:
∵EF⊥AC、∠AEF = β,
∴∠EAF = 90° - ∠AEF = 90° - β.
∵AE平分∠BAC,
∴∠BAE = ∠EAF = 90° - β,
∴∠BAD = ∠BAE - ∠DAE = 90° - β - α.
∵AD⊥BC,
∴∠B = 90° - ∠BAD,即∠B = 90° - (90° - β - α) = α + β.
∵EF⊥AC、∠AEF = β,
∴∠EAF = 90° - ∠AEF = 90° - β.
∵AE平分∠BAC,
∴∠BAE = ∠EAF = 90° - β,
∴∠BAD = ∠BAE - ∠DAE = 90° - β - α.
∵AD⊥BC,
∴∠B = 90° - ∠BAD,即∠B = 90° - (90° - β - α) = α + β.
16. 如图,在$\triangle ABC$中,$∠B = ∠C = 45°$,点$D$,$E$分别在边$BC$,$AC$上,且$∠ADE = ∠AED$.
(1) 当$∠BAD = 60°$时,求$∠CDE$的度数;
(2)当点$D$在边$BC$上(点$B$,$C$除外)运动时,试写出$∠BAD$与$∠CDE$之间的数量关系,并说明理由.
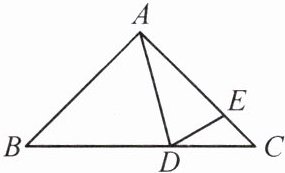
(1) 当$∠BAD = 60°$时,求$∠CDE$的度数;
(2)当点$D$在边$BC$上(点$B$,$C$除外)运动时,试写出$∠BAD$与$∠CDE$之间的数量关系,并说明理由.

答案:
16.解:
(1)
∵∠B = ∠C = 45°,
∴∠BAC = 90°,
∴∠DAC = ∠BAC - ∠BAD = 90° - 60° = 30°.
∵∠ADE = ∠AED,
∴∠ADE = $\frac{1}{2}$(180° - ∠DAC) = 75°.又∠ADC = ∠B + ∠BAD = 45° + 60° = 105°,
∴∠CDE = ∠ADC - ∠ADE = 105° - 75° = 30°.
(2)∠CDE = $\frac{1}{2}$∠BAD.理由如下:设∠BAD = x.由
(1)可得∠DAC = 90° - x,
∴∠ADE = $\frac{1}{2}$(180° - ∠DAC) = $\frac{1}{2}$(180° - 90° + x) = 45° + $\frac{1}{2}$x.又∠ADC = ∠B + ∠BAD = 45° + x,
∴∠CDE = ∠ADC - ∠ADE = 45° + x - (45° + $\frac{1}{2}$x) = $\frac{1}{2}$x,即∠CDE = $\frac{1}{2}$∠BAD.
(1)
∵∠B = ∠C = 45°,
∴∠BAC = 90°,
∴∠DAC = ∠BAC - ∠BAD = 90° - 60° = 30°.
∵∠ADE = ∠AED,
∴∠ADE = $\frac{1}{2}$(180° - ∠DAC) = 75°.又∠ADC = ∠B + ∠BAD = 45° + 60° = 105°,
∴∠CDE = ∠ADC - ∠ADE = 105° - 75° = 30°.
(2)∠CDE = $\frac{1}{2}$∠BAD.理由如下:设∠BAD = x.由
(1)可得∠DAC = 90° - x,
∴∠ADE = $\frac{1}{2}$(180° - ∠DAC) = $\frac{1}{2}$(180° - 90° + x) = 45° + $\frac{1}{2}$x.又∠ADC = ∠B + ∠BAD = 45° + x,
∴∠CDE = ∠ADC - ∠ADE = 45° + x - (45° + $\frac{1}{2}$x) = $\frac{1}{2}$x,即∠CDE = $\frac{1}{2}$∠BAD.
17. 如图,在$\triangle ABC$中,$∠ACB = 90°$,$AC = BC$,$D$是线段$AB$上一动点,$DE$,$DF$分别交$BC$,$AC$的延长线于点$E$,$F$,且$∠ADE = ∠BDF$,作$∠GEH = ∠BED$(点$H$在$BC$的延长线上),试判断直线$GE$与直线$DF$的位置关系,并说明理由.
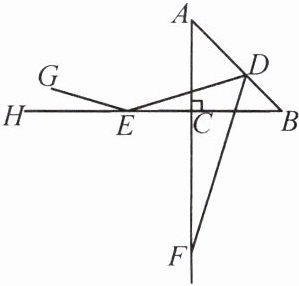

答案:
17.解:GE⊥DF.理由如下:
∵∠ACB = 90°,AC = BC,
∴∠B = 45°.设∠ADE = ∠BDF = α,∠GEH = ∠BED = β.如图,

延长GE交DF于点M,则∠BEM = ∠GEH = β.
∵∠EDM = 180° - 2α,∠DEM = ∠BED + ∠BEM = 2β,
∴∠EMD = 180° - ∠EDM - ∠DEM = 180° - (180° - 2α) - 2β = 2(α - β).又∠ADE = ∠BED + ∠B,即α = β + 45°,
∴α - β = 45°,
∴∠EMD = 2×45° = 90°,
∴GE⊥DF.
17.解:GE⊥DF.理由如下:
∵∠ACB = 90°,AC = BC,
∴∠B = 45°.设∠ADE = ∠BDF = α,∠GEH = ∠BED = β.如图,

延长GE交DF于点M,则∠BEM = ∠GEH = β.
∵∠EDM = 180° - 2α,∠DEM = ∠BED + ∠BEM = 2β,
∴∠EMD = 180° - ∠EDM - ∠DEM = 180° - (180° - 2α) - 2β = 2(α - β).又∠ADE = ∠BED + ∠B,即α = β + 45°,
∴α - β = 45°,
∴∠EMD = 2×45° = 90°,
∴GE⊥DF.
查看更多完整答案,请扫码查看


