1. 下列计算中,结果是 $ a^{6} $ 的是(
A.$ a^{2}+a^{4} $
B.$ a^{2} \cdot a^{3} $
C.$ a^{12} ÷ a^{2} $
D.$ (a^{2})^{3} $
D
)A.$ a^{2}+a^{4} $
B.$ a^{2} \cdot a^{3} $
C.$ a^{12} ÷ a^{2} $
D.$ (a^{2})^{3} $
答案:
1.D
2. 如图①,将一张长方形铁片四角各切去一个同样的正方形,制成如图②所示的无盖铁盒.若该铁盒的容积为 $ 2a^{2}b $,则该铁盒底面的周长为(
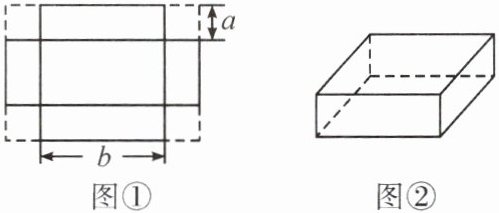
A.$ 2ab $
B.$ 4ab $
C.$ 2a + b $
D.$ 4a + 2b $
D
)
A.$ 2ab $
B.$ 4ab $
C.$ 2a + b $
D.$ 4a + 2b $
答案:
2.D
3. 下列运算中,错误的有(
① $ (2x + y)(-2x - y) = 4x^{2} - y^{2} $;
② $ (a - 3b)(3b + a) = a^{2} - 3b^{2} $;
③ $ (-x - y)^{2} = x^{2} - 2xy + y^{2} $;
④ $ (x - \frac{1}{2})^{2} = x^{2} - x + \frac{1}{4} $.
A.1 个
B.2 个
C.3 个
D.4 个
C
)① $ (2x + y)(-2x - y) = 4x^{2} - y^{2} $;
② $ (a - 3b)(3b + a) = a^{2} - 3b^{2} $;
③ $ (-x - y)^{2} = x^{2} - 2xy + y^{2} $;
④ $ (x - \frac{1}{2})^{2} = x^{2} - x + \frac{1}{4} $.
A.1 个
B.2 个
C.3 个
D.4 个
答案:
3.C
4. 已知 $ (mx - y)^{2} = 4x^{2} - 4xy + ny^{2} $,则 $ \frac{m}{n} $ 的值为(
A.-2
B.2
C.$ -\frac{1}{2} $
D.$ \frac{1}{2} $
B
)A.-2
B.2
C.$ -\frac{1}{2} $
D.$ \frac{1}{2} $
答案:
4.B
5. 已知 $ M = 2024^{2},N = 2023 × 2025 $,则 $ (N - M)^{2025} $ 的值是(
A.1
B.-1
C.2025
D.-2025
B
)A.1
B.-1
C.2025
D.-2025
答案:
5.B
6. 计算 $ (m - 2n - 1)(m + 2n - 1) $ 的结果是(
A.$ m^{2} - 4n^{2} - 2m + 1 $
B.$ m^{2} + 4n^{2} - 2m + 1 $
C.$ m^{2} - 4n^{2} + 2m - 1 $
D.$ m^{2} + 4n^{2} + 2m - 1 $
A
)A.$ m^{2} - 4n^{2} - 2m + 1 $
B.$ m^{2} + 4n^{2} - 2m + 1 $
C.$ m^{2} - 4n^{2} + 2m - 1 $
D.$ m^{2} + 4n^{2} + 2m - 1 $
答案:
6.A
7. 若 $ x^{2} + 12x - 1 = 0 $,则 $ 2(x - 3)^{2} - 3(x + 1)(x - 1) $ 的值为(
A.18
B.20
C.22
D.24
B
)A.18
B.20
C.22
D.24
答案:
7.B
8. 已知 $ m $ 是方程 $ x^{2} + 3x - 2022 = 0 $ 的解,则 $ m^{3} + 2m^{2} - 2025m + 2022 $ 的值是(
A.-2022
B.0
C.2022
D.4044
B
)A.-2022
B.0
C.2022
D.4044
答案:
8.B
9. 已知 $ 3^{a} = 5,5^{b} = 9 $,则 $ ab $ 的值是
2
.
答案:
9.2
10. 若 $ (a - 3 - b)(a + 3 - b) = 40 $,则 $ a - b $ 的值是
±7
.
答案:
10.±7
11. 若 $ (m - n)^{2} = 8,(m + n)^{2} = 4 $,则 $ m^{2} + n^{2} $ 的值是
6
.
答案:
11.6
12. 小明计算一道整式乘法题: $ (x - m)(x + 5) $,他把“$ -m $”抄成了“$ +m $”,得到的结果是 $ x^{2} + 11x + n $,则 $ m + n $ 的值为
36
.
答案:
12.36
13. 如图,我国古代数学家赵爽的“勾股弦方图”是由 4 个全等的直角三角形与中间的小正方形拼成的一个大正方形.若大正方形的面积为 13,小正方形的面积为 1,直角三角形的两条直角边的长分别为 $ a,b $,则 $ (a + b)^{2} $ 的值为

25
.

答案:
13.25
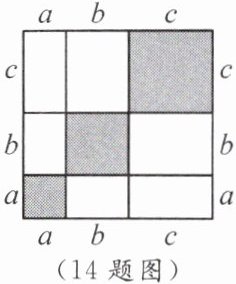
14. (1)利用如图所示的拼图,通过不同方法的面积计算可得出: $ (a + b + c)^{2} = $
(2)若 $ a + b + c = 11,bc + ac + ab = 38 $,则 $ a^{2} + b^{2} + c^{2} = $
a²+b²+c²+2ab+2bc+2ac
;(2)若 $ a + b + c = 11,bc + ac + ab = 38 $,则 $ a^{2} + b^{2} + c^{2} = $
45
.
答案:
14.
(1)a²+b²+c²+2ab+2bc+2ac
(2)45
(1)a²+b²+c²+2ab+2bc+2ac
(2)45
查看更多完整答案,请扫码查看


