《2025年超越训练八年级数学上册人教版四川专版》

8. 在等腰三角形$ABC$中，$AB=AC$，中线$BD$将这个三角形的周长分为15和12两部分，则这个等腰三角形的底边长为(C)

A.7
B.11
C.7或11
D.7或10

答案： 8.C

9. 已知$\triangle ABC$的三边长为3，4，$1-2m$，则$m$的取值范围是-3＜m＜0.

答案： 9.-3＜m＜0

10. 若三角形$ABC$的两边长是方程组$\begin{cases}x+2y=10,\\4x+3y=20\end{cases}$的解，第三边长为整数，则符合条件的三角形有3个.

答案： 10.3

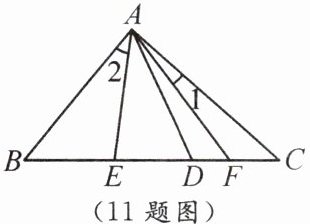
11. 如图，$D$是$\triangle ABC$的边$BC$上任意一点，$AE$是$\angle BAD$的平分线，$AF$是$\angle CAD$的平分线.若$\angle 1+\angle 2=44^{\circ}$，则$\angle B+\angle C=$92°.

答案： 11.92°

12. 如图，在$\triangle ABC$中，$AD$是中线，$DE\perp AB$，垂足为$E$，$DF\perp AC$，垂足为$F$.若$AB=6$，$AC=4$，则$\dfrac{DE}{DF}$的值是$\frac{2}{3}$.

答案： 12.$\frac{2}{3}$

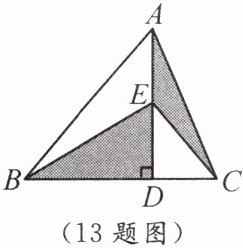
13. 如图，在$\triangle ABC$中，$AD$是高，$CE$是$\triangle ACD$的中线，连接$BE$.若$BD=2CD$，$S_{\triangle ECD}=a$，则图中阴影部分的面积为3a(用含$a$的代数式表示).

答案： 13.3a

14. 如图，在四边形$ABCD$中，点$E$是$\triangle ABD$的重心，点$F$是$\triangle BCD$的重心.若四边形$ABCD$的面积是12，则阴影四边形$DEBF$的面积是4.

答案： 14.4

15. 已知$a$，$b$，$c$是$\triangle ABC$的三边长，且$(b-3)^2+|c-8|=0$.
（1）若$a$是整数，求$\triangle ABC$周长的最小值和最大值；
（2）若$\triangle ABC$是等腰三角形，求$\triangle ABC$的周长.

答案： 15.解：
(1)
∵$(b - 3)^{2}\geq0$，$\vert c - 8\vert\geq0$，
∴$b - 3 = 0$，$c - 8 = 0$，解得$b = 3$，$c = 8$，
∴$8 - 3 ＜ a ＜ 8 + 3$，即$5 ＜ a ＜ 11$。
∵$a$是整数，
∴$a$最小=6，$a$最大=10，
∴△ABC周长的最小值为3+8+6=17，△ABC周长的最大值为3+8+10=21。
(2)①若△ABC的三边长为3，3，8，不符合三角形的三边关系；②若△ABC的三边长为3，8，8，符合三角形的三边关系。
∴△ABC的周长为3+8+8=19。

16. 如图，在平面直角坐标系中，已知点$A(-3,0)$，$B(0,4)$，$AB=5$.按要求作图，并解答问题.
（1）在$x$轴的负半轴上作一点$D$，使得$\triangle ABD$是等腰三角形，并写出点$D$的坐标；
（2）①在$x$轴的正半轴上作一点$E$，使得$\triangle ABE$是直角三角形；
②作$\triangle ABE$的角平分线$AM$，交$y$轴于点$N$，判断$\triangle BMN$的形状，并说明理由.

答案：
16.解：
(1)作图如图所示，点D的坐标为(-8,0)。
(2)①②作图如图所示。△BMN 是等腰三角形，理由如下：
∵∠ABE=∠AOB=90°，
∴∠BMN=90°-∠BAM，∠BNM=∠ANO=90°-∠EAM。
∵AM平分∠BAE，
∴∠BAM=∠EAM，
∴∠BMN=∠BNM，
∴△BMN是等腰三角形。