第61页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
探究性作业 相等吗?
同学们,通过第五单元的学习,我们初步认识感悟并形成了一定的代数观念,观察下面的式子,你觉得它们相等吗?
$a^{2}+b^{2}= (a+b)^{2}$
探究过程:
方法一:举例计算:
1 如果a,b都不是0,可以尝试举例计算,再比较式子的大小。
举例一:当$a= 1,b= 2时a^{2}+b^{2}= (\quad)$ $(a+b)^{2}= (\quad)$
你的举例:当$a= (\quad)$ $b= (\quad)$ $a^{2}+b^{2}= (\quad)$ $(a+b)^{2}= (\quad)$
结论:当a,b都不是0时,$a^{2}+b^{2}\neq(a+b)^{2}$
2 特殊举例:
(1)当$a= 0,b= 1$时呢?当$a= 0,b= 1$,$a^{2}+b^{2}= (\quad)$ $(a+b)^{2}= (\quad)$
(2)当$a= 1,b= 0$时呢?当$a= 1,b= 0$,$a^{2}+b^{2}= (\quad)$ $(a+b)^{2}= (\quad)$
结论:当a,b有一个数是0时,$a^{2}+b^{2}= (a+b)^{2}$
方法二:数形结合
看到$a^{2}$,你想到哪个图形的面积呢?
接下来,我们借助下面的图形,再来研究。
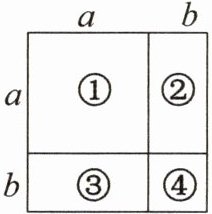
看图分析:$(a+b)$表示大正方形的( ),$(a+b)^{2}$表示大正方形的( ),$a^{2}$表示( )号图形的面积,$b^{2}$表示( )号图形的面积。大正方形的面积是4个图形面积的和。
很明显$(a+b)^{2}>a^{2}+b^{2}$
结论:$(a+b)^{2}>a^{2}+b^{2}$,它们不相等。
探究延伸:迁移类推
同学们,你知道$a^{2}-b^{2}和(a-b)^{2}$相等吗?你能用今天的探究方法继续研究吗?
(1)请你自己尝试举例a和b的具体数值,验证$a^{2}-b^{2}和(a-b)^{2}$的大小关系?
(2)请你结合下图,说明$a^{2}-b^{2}和(a-b)^{2}$的大小关系。

同学们,通过第五单元的学习,我们初步认识感悟并形成了一定的代数观念,观察下面的式子,你觉得它们相等吗?
$a^{2}+b^{2}= (a+b)^{2}$
探究过程:
方法一:举例计算:
1 如果a,b都不是0,可以尝试举例计算,再比较式子的大小。
举例一:当$a= 1,b= 2时a^{2}+b^{2}= (\quad)$ $(a+b)^{2}= (\quad)$
你的举例:当$a= (\quad)$ $b= (\quad)$ $a^{2}+b^{2}= (\quad)$ $(a+b)^{2}= (\quad)$
结论:当a,b都不是0时,$a^{2}+b^{2}\neq(a+b)^{2}$
2 特殊举例:
(1)当$a= 0,b= 1$时呢?当$a= 0,b= 1$,$a^{2}+b^{2}= (\quad)$ $(a+b)^{2}= (\quad)$
(2)当$a= 1,b= 0$时呢?当$a= 1,b= 0$,$a^{2}+b^{2}= (\quad)$ $(a+b)^{2}= (\quad)$
结论:当a,b有一个数是0时,$a^{2}+b^{2}= (a+b)^{2}$
方法二:数形结合
看到$a^{2}$,你想到哪个图形的面积呢?
接下来,我们借助下面的图形,再来研究。

看图分析:$(a+b)$表示大正方形的( ),$(a+b)^{2}$表示大正方形的( ),$a^{2}$表示( )号图形的面积,$b^{2}$表示( )号图形的面积。大正方形的面积是4个图形面积的和。
很明显$(a+b)^{2}>a^{2}+b^{2}$
结论:$(a+b)^{2}>a^{2}+b^{2}$,它们不相等。
探究延伸:迁移类推
同学们,你知道$a^{2}-b^{2}和(a-b)^{2}$相等吗?你能用今天的探究方法继续研究吗?
(1)请你自己尝试举例a和b的具体数值,验证$a^{2}-b^{2}和(a-b)^{2}$的大小关系?
(2)请你结合下图,说明$a^{2}-b^{2}和(a-b)^{2}$的大小关系。

答案:
1. 5 9 3 4 25 49(答案不唯一)
2.(1)1 1 (2)1 1 边长 面积 ① ④
(1)(举例计算,答案不唯一)
当$a = 0$,$b = 0$时,$(a - b)^2=0$ $a^2 - b^2=0$ $a^2-b^2=(a - b)^2$
当$a = 2$,$b = 0$时,$(a - b)^2 = 4$ $a^2 - b^2=4$ $a^2-b^2=(a - b)^2$
结论:当$a$,$b$有一个数是0时($a$大于或等于$b$),
$a^2 - b^2=(a - b)^2$
当$a = 2$,$b = 1$时,$(a - b)^2=1$ $a^2 - b^2=3$($a-b)^2\lt a^2 - b^2$
(2)$(a - b)^2$表示图中④号图形的面积,
$a^2 - b^2$表示图中②号、③号与④号图形的面积之和,所以$(a - b)^2\lt a^2 - b^2$。
2.(1)1 1 (2)1 1 边长 面积 ① ④
(1)(举例计算,答案不唯一)
当$a = 0$,$b = 0$时,$(a - b)^2=0$ $a^2 - b^2=0$ $a^2-b^2=(a - b)^2$
当$a = 2$,$b = 0$时,$(a - b)^2 = 4$ $a^2 - b^2=4$ $a^2-b^2=(a - b)^2$
结论:当$a$,$b$有一个数是0时($a$大于或等于$b$),
$a^2 - b^2=(a - b)^2$
当$a = 2$,$b = 1$时,$(a - b)^2=1$ $a^2 - b^2=3$($a-b)^2\lt a^2 - b^2$
(2)$(a - b)^2$表示图中④号图形的面积,
$a^2 - b^2$表示图中②号、③号与④号图形的面积之和,所以$(a - b)^2\lt a^2 - b^2$。
查看更多完整答案,请扫码查看


