《2025年1课3练单元达标测试五年级数学上册苏教版》

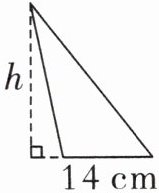
1. 林林早餐吃的三明治从上面看近似一个三角形,如右边的示意图,已知三角形的面积为 $168\ cm^2$,则三角形的高 $h$ 为( )cm。

答案： 24 [提示]168×2÷14=24(cm)

2. 计算下面各三角形的面积。
(1)

(2)
(3)

答案：
(1)12×7÷2=42(cm²)；
(2)9×8÷2=36(cm²)；
(3)14×8÷2=56(cm²) [提示]三角形的面积=底×高÷2

3. 一块三角形的玻璃被打碎了,已知原来三角形玻璃的面积是 220 平方厘米,底是 20 厘米。你能算出原来这块三角形玻璃的高是多少厘米吗？

答案： 220×2÷20=22(厘米) [提示]已知三角形的面积和底,根据三角形的面积公式:S=a×h÷2,用三角形的面积乘2,然后除以底,得到三角形的高。

4. 新情境 冰雕展览 每年冬季,冰城哈尔滨都会举行冰雕展览。冰雕艺术作为冰雪文化的重要组成部分,不仅彰显着地域特色,还是一种文化传承,更是哈尔滨的亮丽名片。一位冰雕大师在一块直角三角形的冰块上雕了一件作品,这块冰块三条边的长度分别是 30 分米、40 分米和 50 分米。这块冰块的面积是多少平方分米？

答案： 30×40÷2=600(平方分米) [提示]已知直角三角形三条边的长度,可知两条直角边的长度分别是30分米和40分米,根据三角形的面积公式“S=a×h÷2”求出这块冰块的面积即可。

5. 原创题 几何直观 数学社团会开展各种各样的数学游戏和挑战,每次活动都像是一场智力冒险,深受孩子们的喜爱。在一次数学社团活动中,李老师出了一道有趣的题目：右下图是由一个边长为 8 厘米的正方形和一个边长为 6 厘米的正方形拼成的,你会求涂色部分的面积吗？
涂色部分三角形的底是小正方形的边长,高是大正方形的边长。
]

答案： 6×8÷2=24(平方厘米) [提示]涂色部分三角形的底是小正方形的边长,高是大正方形的边长。