第15页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
1. 求下面各图形的面积。(单位:分米)
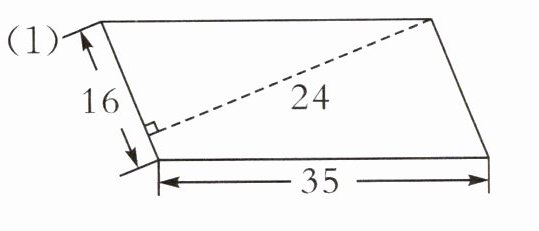
(1)
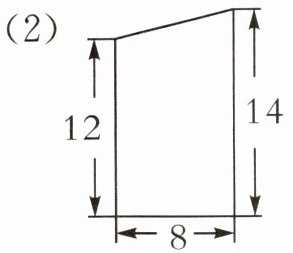
(2)
(3)

(1)

(2)

(3)

答案:
1.
(1)16×24=384(平方分米)[提示]根据“平行四边形的面积=底×高”列式解答。
(2)(12+14)×8÷2=104(平方分米)[提示]根据“梯形的面积=(上底+下底)×高÷2”列式解答。
(3)9×12÷2=54(平方分米) [提示]根据“三角形的面积=底×高÷2”列式解答。
(1)16×24=384(平方分米)[提示]根据“平行四边形的面积=底×高”列式解答。
(2)(12+14)×8÷2=104(平方分米)[提示]根据“梯形的面积=(上底+下底)×高÷2”列式解答。
(3)9×12÷2=54(平方分米) [提示]根据“三角形的面积=底×高÷2”列式解答。
2. 等腰梯形的周长是 48 cm,面积是$ 96 cm^2,$高是 6 cm,则它的一条腰长是( )cm。
A.8
B.12
C.14
D.18
A.8
B.12
C.14
D.18
答案:
2. A [提示]梯形上底与下底的和=面积×2÷高,即上底+下底=96×2÷6=32(cm),等腰梯形的一条腰长=(周长-上底-下底)÷2=[周长-(上底+下底)]÷2=(48-32)÷2=8(cm)。
3. 新情境 银杏 银杏有“活化石”的美称,银杏树的果实俗称白果,因此银杏树又名白果树。我国的“银杏之乡”泰兴有一片梯形银杏园,上底是 40 米,下底是 60 米,高是 50 米。这片银杏园里种了100 棵银杏树,平均每棵银杏树占地多少平方米?
答案:
3. (40+60)×50÷2=2500(平方米)2500÷100=25(平方米) [提示]先计算出梯形银杏园的面积,再用面积除以银杏树的棵数,求出平均每棵银杏树的占地面积。
4. 新考法 评价说明 护林员在巡山过程中,发现山腰一侧的树木稀少,泥土下滑,很容易给山底下的村民带来安全隐患,因此负责人决定种植树木。已知这座树木稀少的山体表面近似一个梯形,其中高和上底的积是 29 平方米,高和下底的积是 79 平方米。近似梯形的山体的面积是多少平方米? 通过护林员的发现,你有什么建议想对大家说的吗?
答案:
4. (29+79)÷2=54(m²) [提示]梯形的面积为(上底+下底)×高÷2=(上底×高+下底×高)÷2。答案不唯一,如:多宣传种树的益处,在小区公告栏里警示人们乱砍滥伐的危害,从而激起人们保护树木的意识与责任。要节约使用一次性筷子、火柴、纸张等物品,这样可以减少树木的消耗量和砍伐量,从而保护树木。 [提示]合理即可。
5. 新情境 观日桥 某市在临海公园修了一座观日桥,早晨站在桥面上可以第一时间看到日出的美丽景观。这座桥的横截面是如右下图所示的梯形,梯形的下底是 18 米,高是 5 米,两个底角都是45°,求梯形的面积。
先求出梯形的上底是多少。

先求出梯形的上底是多少。

答案:
5. 18-5-5=8(米) (8+18)×5÷2=65(平方米)[提示]因为梯形的两个底角都是45°,所以两个小三角形都是等腰直角三角形,可以求出梯形的上底是18-5-5=8(米),再根据梯形的面积公式计算即可解答。
查看更多完整答案,请扫码查看


