《2025年名校课堂九年级数学上册人教版安徽专版》

14. (2024·安徽)已知抛物线$y=-x^{2}+bx(b$为常数)的顶点横坐标比抛物线$y=-x^{2}+2x$的顶点横坐标大$1$.
(1)求$b$的值.
(2)点$A(x_{1},y_{1})$在抛物线$y=-x^{2}+2x$上,点$B(x_{1}+t,y_{1}+h)$在抛物线$y=-x^{2}+bx$上.
①若$h=3t$,且$x_{1}≥0,t＞0$,求$h$的值.
②若$x_{1}=t-1$,求$h$的最大值.

答案： 解:
(1)
∵抛物线y=-x²+bx的顶点横坐标为$\frac{b}{2}$,y=-x²+2x的顶点横坐标为1,
∴$\frac{b}{2}-1=1$.
∴b=4.
(2)
∵点A(x₁,y₁)在抛物线y=-x²+2x上,
∴y₁=-x₁²+2x₁.
∵点B(x₁+t,y₁+h)在抛物线y=-x²+4x上,
∴y₁+h=-(x₁+t)²+4(x₁+t).
∴-x₁²+2x₁+h=-(x₁+t)²+4(x₁+t).
∴h=-t²-2x₁t+2x₁+4t.①
∵h=3t,
∴3t=-t²-2x₁t+2x₁+4t.
∴t(t+2x₁)=t+2x₁.
∵x₁≥0,t＞0,
∴t+2x₁＞0.
∴t=1.
∴h=3.②将x₁=t-1代入h=-t²-2x₁t+2x₁+4t,得h=-3t²+8t-2,
∴h=-3$(t-\frac{4}{3})^{2}+\frac{10}{3}$.
∵-3＜0,
∴当t=$\frac{4}{3}$,即x₁=$\frac{1}{3}$时,h取最大值$\frac{10}{3}$.

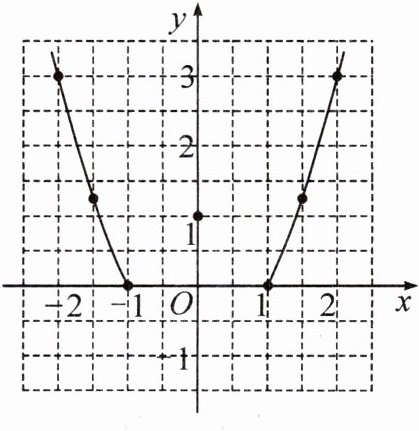
15. 新考向 过程性学习 九年级某班成立了数学学习兴趣小组,该小组对函数$y=|x^{2}-1|$的图象和性质进行探究,过程如下,请你补充完整.
(1)①列表:下表是$x,y$的几组对应值,其中$m=$$\frac{3}{4}$,$n=$$\frac{3}{4}$.

②描点:根据表中的数值描点$(x,y)$,请补充描出点$(-\frac{1}{2},m),(\frac{1}{2},n)$.
③连线:用平滑的曲线顺次连接各点,请把图象补充完整.
(2)请观察图象,直接写出当$y$随$x$的增大而增大时,$x$的取值范围为-1＜x＜0或x＞1.
(3)除了上述增减性,请你再写出两条该函数的图象特征或性质:
①函数图象是轴对称图形;
②函数值y都是非负数.
(4)若点$(m,a)$与$(n,b)$在函数图象上,且$|n|＜|m|＜1$,则$a$与$b$的大小关系是a＜b.

答案： 解:
(1)①$\frac{3}{4}$ $\frac{3}{4}$ ②补充描点略.③补全图象略.
(2)-1＜x＜0或x＞1
(3)①函数图象是轴对称图形 ②函数值y都是非负数
(4)a＜b