《2025年暑假园地知识出版社四年级数学苏教版》

1. 简便方法计算 $ 136 + 258 + 64 $,要先算$136 + 64$,这是应用了加法交换律和加法结合律。

答案： $136 + 64$ 加法交换律和加法结合律

$37 + 15 = 15 + 37$ $54 + 48 + 22 = 54 + (48 + 22)$ $(27 + 44) + 56 = 27 + (44 + 56)$ $b + (37 + 88) = (b + 88) + 37$

答案： $37 + 15 = 15 + 37$
$54 + 48 + 22 = 54 + (48 + 22)$
$(27 + 44) + 56 = 27 + (44 + 56)$
$b + (37 + 88) = (b + 88) + 37$

3. 如果 $ x + y = 300 $,且 $ x - y = 150 $,那么 $ x + (y + 40) = (340)$,$ x - (y - 60) = (210) $。

答案： 解：
由 $x + y = 300$，$x - y = 150$，
对于 $x + (y + 40)$：
$x + (y + 40) = (x + y) + 40 = 300 + 40 = 340$；
对于 $x - (y - 60)$：
$x - (y - 60) = (x - y) + 60 = 150 + 60 = 210$。
340 210

1. $ 43 + 65 + 57 + 35 = (43 + 57) + (65 + 35) $的根据是(C)。
A.加法交换律
B.加法结合律
C.加法交换律和结合律
D.无法判断

答案： $43 + 65 + 57 + 35$，先交换$65$和$57$的位置，变为$43 + 57 + 65 + 35$，这一步运用了加法交换律；再分别将$43$与$57$、$65$与$35$结合相加，即$(43 + 57) + (65 + 35)$，这一步运用了加法结合律。所以该等式的根据是加法交换律和结合律。
C

2. $ 347 - 98 $用简便方法计算是(C)。
A.$ 347 - 100 - 2 $
B.$ 347 - (100 + 2) $
C.$ 347 - 100 + 2 $
D.$ 347 - 90 + 8 $

答案： 解：$347 - 98$
$= 347 - (100 - 2)$
$= 347 - 100 + 2$
答案：C

3. 与 $ ☆ - (\triangle + □) $结果相等的算式是(C)。
A.$ ☆ - \triangle + □ $
B.$ ☆ + \triangle - □ $
C.$ ☆ - \triangle - □ $
D.$ ☆ + \triangle + □ $

答案： 根据减法的性质：一个数减去两个数的和，等于这个数连续减去这两个数。
所以$☆ - (\triangle + □) = ☆ - \triangle - □$。
答案：C

三、将和是整百或整千的两只青蛙连在一起。

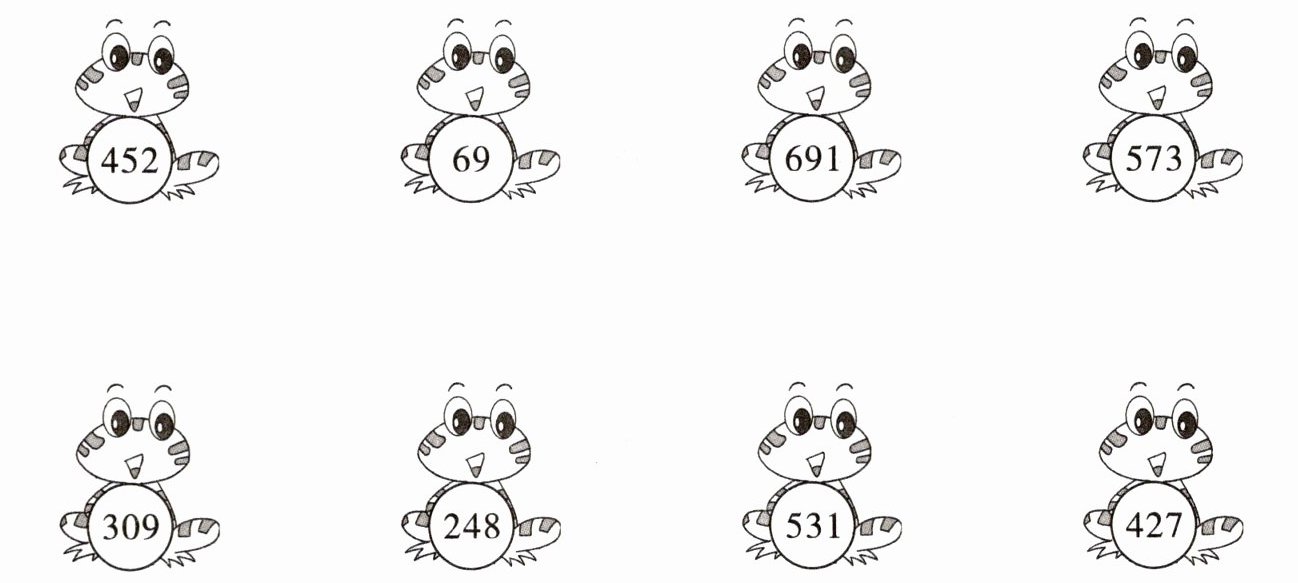
答案： 452—248
69—531
691—309
573—427