《2025年暑假园地知识出版社四年级数学苏教版》

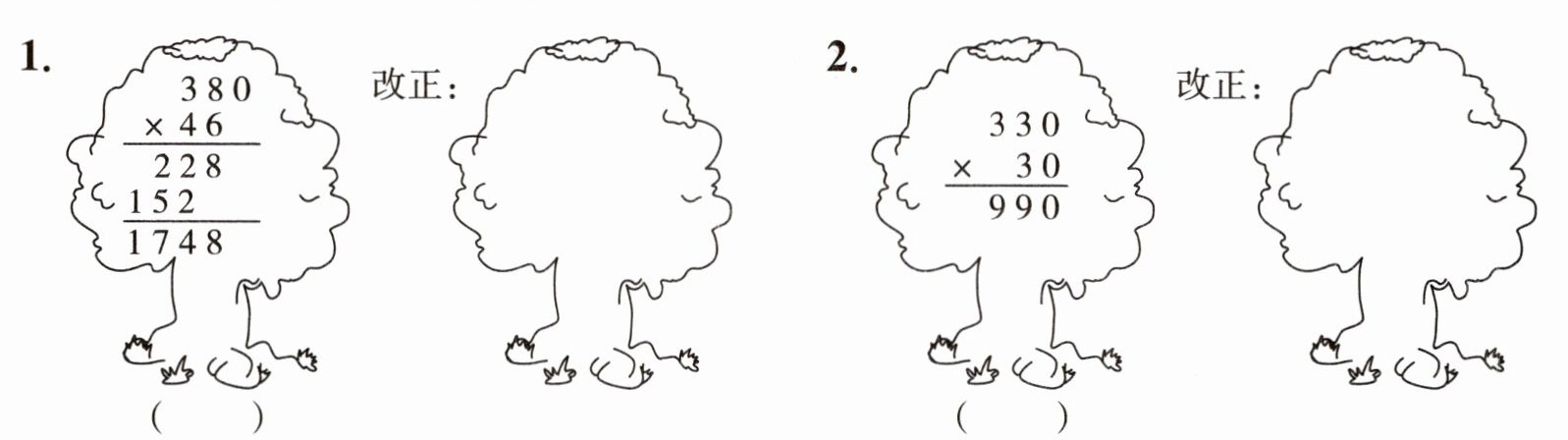
四、判一判。(对的画“√”,错的画“×”,并改正)

答案：
1. × 2. ×

1. 某商场举行“冬季温暖特卖会”,一款热销羽绒服每件 450 元,某天共卖出 90 件,上午卖出 35 件,下午比上午多卖多少元?

答案： 下午卖出的件数：$90 - 35 = 55$（件）
下午比上午多卖的件数：$55 - 35 = 20$（件）
下午比上午多卖的金额：$450×20 = 9000$（元）
答：下午比上午多卖9000元。

2. 妙妙在计算一道乘数末尾只有一个 0 的乘法算式时,忘记在积的末尾添上 0,结果比正确的积少 315,正确的积是多少?

答案： 解：315÷(10 - 1) = 35
35×10 = 350
答：正确的积是350。

两箱姜
买来七十二块姜,放进大小两纸箱;
大箱放多小箱少,两箱块数不一样;
大箱每次拿三块,拿来放入小纸箱;
拿出放进共五次,两箱块数才等量。
猜一猜,想一想,两箱原放几块姜?

答案： 解析：本题可通过设未知数，根据题目中的数量关系列出方程求解。
设大箱原来放$x$块姜，小箱原来放$y$块姜。
步骤一：分析题目中的数量关系
已知买来$72$块姜放进大小两纸箱，则可得到$x + y = 72$。
又已知大箱每次拿$3$块放入小箱，拿了$5$次后两箱块数一样多，那么大箱拿出$3×5 = 15$块，此时大箱有$(x - 15)$块；小箱放入$15$块，此时小箱有$(y + 15)$块，可得到$x - 15 = y + 15$。
步骤二：联立方程求解
联立方程组$\begin{cases}x + y = 72\\x - 15 = y + 15\end{cases}$
由$x - 15 = y + 15$可得$x - y = 30$，即$x = y + 30$。
将$x = y + 30$代入$x + y = 72$中，得到$(y + 30) + y = 72$。
去括号得$y + 30 + y = 72$，
合并同类项得$2y + 30 = 72$，
移项得$2y = 72 - 30$，
计算得$2y = 42$，
两边同时除以$2$得$y = 21$。
将$y = 21$代入$x = y + 30$，可得$x = 21 + 30 = 51$。
答案：大箱原放$51$块姜，小箱原放$21$块姜。