《2025年阳光假日暑假四年级数学人教版》

2. 如图，已知$∠4=55^{\circ },∠6=130^{\circ }$，求$∠2$和$∠7$的度数。

$∠2=$$35^{\circ}$，$∠7=$$50^{\circ}$

答案： 【解析】：
- 求$∠2$的度数：
因为三角形内角和为$180^{\circ}$，在含有$∠2$、$∠4$的直角三角形中，$∠2 = 180^{\circ}-90^{\circ}-∠4$。
已知$∠4 = 55^{\circ}$，则$∠2=180^{\circ}-90^{\circ}-55^{\circ}=35^{\circ}$。
求$∠7$的度数：
四边形内角和为$360^{\circ}$，在含有$∠6$、$∠7$的四边形中（有两个直角），$∠7=360^{\circ}-90^{\circ}-90^{\circ}-∠6$。
已知$∠6 = 130^{\circ}$，则$∠7 = 360^{\circ}-90^{\circ}-90^{\circ}-130^{\circ}=50^{\circ}$。
【答案】：$∠2 = 35^{\circ}$，$∠7 = 50^{\circ}$

3. 如图，在正方形$ABCD$中，将正方形的点$A$和点$B$向内折起，使得顶点$A$，$B$重合于点$G$，求$∠CGD$的度数。

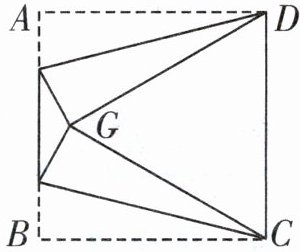
$60^{\circ}$

答案： 【解析】：
- 因为正方形$ABCD$，所以$AD = BC = CD$，$\angle ADC=\angle BCD = 90^{\circ}$。
- 由折叠可知$AD = DG$，$BC = CG$。
- 所以$DG = CG = CD$。
- 因为$DG = CG = CD$，所以$\triangle CGD$是等边三角形。
- 根据等边三角形的性质，等边三角形的三个内角都相等，且都等于$60^{\circ}$，所以$\angle CGD=60^{\circ}$。
【答案】：$60^{\circ}$