《2025年阳光假日暑假四年级数学人教版》

1. 三只小猪盖房子,房顶设计成了三角形,其中两边的长度都是5米,你知道第三条边最短可以多长吗?(三边的长度都是整米数)

答案： 【解析】：根据三角形的三边关系“任意两边之和大于第三边，任意两边之差小于第三边”。已知三角形其中两边的长度都是$5$米，那么两边之和为$5 + 5 = 10$米，两边之差为$5 - 5 = 0$米。所以第三边的长度大于$0$米且小于$10$米，又因为三边的长度都是整米数，所以第三条边最短是$1$米。
【答案】：$1$米

2. 小明要为爷爷的菜地设计篱笆,他想到了几种方案(如下图)。你建议他使用哪种方案?说明你的理由。

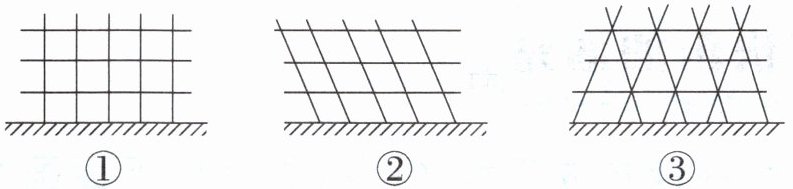
建议使用方案③。理由是三角形具有稳定性，用这种方案设计的篱笆更牢固。

答案： 【解析】：三角形具有稳定性，而长方形（图①）和平行四边形（图②）具有不稳定性，容易变形。图③中含有三角形结构。
【答案】：建议使用方案③。理由是三角形具有稳定性，用这种方案设计的篱笆更牢固。

九、每个图形中有多少个三角形?

（6）；（12）；（6）

答案： 【解析】：
第一个图形：
单个三角形有$3$个，由两个三角形组成的三角形有$2$个，由三个三角形组成的三角形有$1$个，所以三角形总数为$3 + 2 + 1=6$个。
第二个图形：
先看小三角形，单个小三角形有$3$个，由两个小三角形组成的三角形有$2$个，由三个小三角形组成的三角形有$1$个；再看由横线分割出的大三角形，同样单个大三角形有$3$个，由两个大三角形组成的三角形有$2$个，由三个大三角形组成的三角形有$1$个。所以三角形总数为$(3 + 2 + 1)+(3 + 2 + 1)=12$个。
第三个图形：
单个三角形有$3$个，由两个三角形组成的三角形有$2$个，由三个三角形组成的三角形有$1$个，所以三角形总数为$3 + 2 + 1 = 6$个。
【答案】：$6$；$12$；$6$