《2025年阳光假日暑假四年级数学人教版》

4. 下面(C)算式是正确的。
A. $1×4 + 6×9 = 1×6 + 4×9$
B. $(25 + 56)×4 = 25×4 + 56$
C. $64 + 72 + 36 = (64 + 36) + 72$

答案： C

5. $700÷4÷25$的简便算法是(A)。
A. $700÷(4×25)$
B. $700÷25÷4$
C. $700÷(25÷4)$

答案： A

三、配桌椅。(连一连)

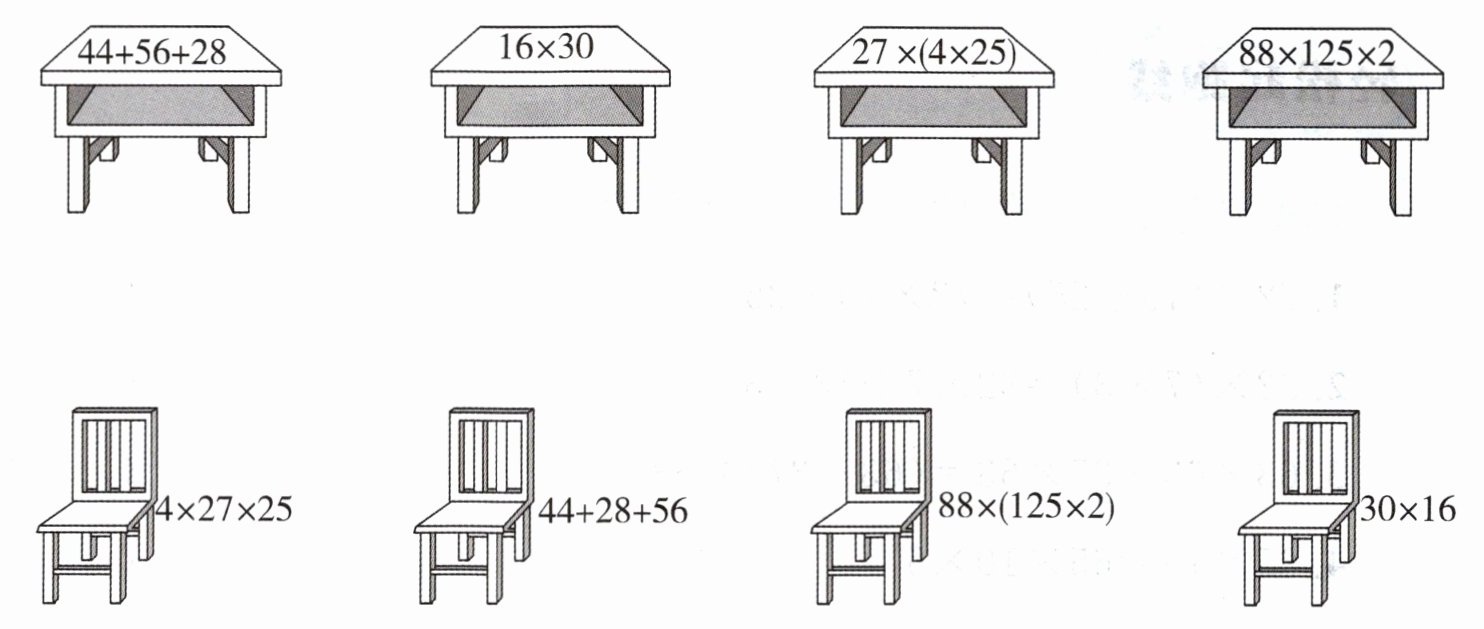
$44 + 56 + 28$连$44 + 28 + 56$；$16×30$连$30×16$；$27×(4×25)$连$4×27×25$；$88×125×2$连$88×(125×2)$

答案： 【解析】：根据加法交换律$a + b = b + a$，$44 + 56 + 28$与$44 + 28 + 56$相连；根据乘法交换律$a×b = b×a$，$16×30$与$30×16$相连；根据乘法结合律$(a×b)×c = a×(b×c)$，$27×(4×25)$与$4×27×25$相连，$88×125×2$与$88×(125×2)$相连。
【答案】：$44 + 56 + 28$连$44 + 28 + 56$；$16×30$连$30×16$；$27×(4×25)$连$4×27×25$；$88×125×2$连$88×(125×2)$。

四、用乘法运算律计算下面各题。
$25×(8 + 4)$ $8×(13×5)$
$67×36 + 67×64$ $238×7 + 7×62$
$99×101$ $125×12 - 125×4$

答案： 【解析】：
1. 对于$25×(8 + 4)$：
根据乘法分配律$a\times(b + c)=a\times b+a\times c$，这里$a = 25$，$b = 8$，$c = 4$。
则$25×(8 + 4)=25×8+25×4=200 + 100=300$。
2. 对于$8×(13×5)$：
根据乘法交换律和结合律$a\times(b\times c)=(a\times c)\times b$，这里$a = 8$，$b = 13$，$c = 5$。
则$8×(13×5)=(8×5)×13=40×13 = 520$。
3. 对于$67×36 + 67×64$：
根据乘法分配律的逆运算$a\times b+a\times c=a\times(b + c)$，这里$a = 67$，$b = 36$，$c = 64$。
则$67×36 + 67×64=67×(36 + 64)=67×100=6700$。
4. 对于$238×7 + 7×62$：
根据乘法分配律的逆运算$a\times b+a\times c=a\times(b + c)$，这里$a = 7$，$b = 238$，$c = 62$。
则$238×7 + 7×62=7×(238 + 62)=7×300=2100$。
5. 对于$99×101$：
把$101$写成$(100 + 1)$，再根据乘法分配律$a\times(b + c)=a\times b+a\times c$，这里$a = 99$，$b = 100$，$c = 1$。
则$99×101=99×(100 + 1)=99×100+99×1=9900+99 = 9999$。
6. 对于$125×12 - 125×4$：
根据乘法分配律的逆运算$a\times b - a\times c=a\times(b - c)$，这里$a = 125$，$b = 12$，$c = 4$。
则$125×12 - 125×4=125×(12 - 4)=125×8=1000$。
【答案】：$300$；$520$；$6700$；$2100$；$9999$；$1000$