《2025年暑假课程练习南方出版社四年级数学》

1. 在一个三角形中，如果三条边都相等，那么这个三角形是(等边三角形)。

答案： 等边三角形

2. 一个等腰三角形，腰为$3$厘米，底为$7$厘米，则它的周长为(13)厘米。

答案： 13

3. 拼成长方形的两个三角形是(完全一样的直角)三角形；拼成正方形的两个三角形是(完全一样的等腰直角)三角形。

答案： 完全一样的直角；完全一样的等腰直角

4. 一个直角三角形中，如果其中一个角是$30^{\circ}$，那么另外两个角是($90^{\circ}$)和($60^{\circ}$)。

答案： $90^{\circ}$ $60^{\circ}$

5. 在直角三角形中，两个锐角的和是(90°)。

答案： 90°

6. 三角形按角分可以分为(锐角)三角形，(直角)三角形，(钝角)三角形。

答案： 锐角 直角 钝角

二、判断。(对的画“√”，错的画“×”)
1. 等腰三角形不可能是直角三角形。(×)
2. 三角形任意一条边的长度不一定小于另两条边长度的和。(×)
3. 任何一个三角形都有3条高。(√)

答案： 1.× 2.× 3.√

1. 在三角形中，已知$\angle1 = 70^{\circ}$，$\angle2 = 95^{\circ}$，求$\angle3$的度数。$\angle3$的度数是$15^{\circ}$。

答案： 【解析】：因为三角形的内角和是$180^{\circ}$，已知三角形中两个角$\angle1 = 70^{\circ}$，$\angle2 = 95^{\circ}$，那么求$\angle3$的度数，用$180^{\circ}$依次减去$\angle1$与$\angle2$的度数即可，即$\angle3=180^{\circ}-\angle1 - \angle2=180^{\circ}-70^{\circ}-95^{\circ}=15^{\circ}$。
【答案】：$15^{\circ}$

2. 已知$\angle1$和$\angle2$是同一直角三角形的两个锐角，$\angle1 = 37^{\circ}$，求$\angle2$的度数。

答案： 【解析】：因为直角三角形的两个锐角和为$90^{\circ}$，已知$\angle1$和$\angle2$是同一直角三角形的两个锐角，$\angle1 = 37^{\circ}$，那么$\angle2=90^{\circ}-\angle1 = 90^{\circ}-37^{\circ}=53^{\circ}$。
【答案】：$53^{\circ}$

3. 已知等腰三角形的底角是$50^{\circ}$，它的顶角是多少度？

答案： 【解析】：因为等腰三角形的两个底角相等，三角形的内角和是180°，已知底角是50°，那么用180°减去两个底角的度数和就能得到顶角的度数，即180° - 50°×2 = 180° - 100° = 80°。
【答案】：80°

4. 已知$\angle1 = 60^{\circ}$，$\angle2 = 50^{\circ}$。求$\angle3$和$\angle4$的度数。

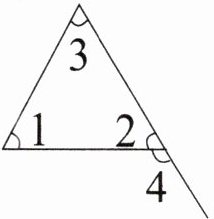
$\angle3=$$70^{\circ}$，$\angle4=$$130^{\circ}$

答案： 【解析】：
- 求$\angle3$的度数：
因为三角形内角和为$180^{\circ}$，已知$\angle1 = 60^{\circ}$，$\angle2 = 50^{\circ}$，所以$\angle3=180^{\circ}-\angle1 - \angle2$。
即$\angle3 = 180^{\circ}-60^{\circ}-50^{\circ}=70^{\circ}$。
求$\angle4$的度数：
因为$\angle2$与$\angle4$组成平角，平角为$180^{\circ}$，所以$\angle4 = 180^{\circ}-\angle2$。
即$\angle4 = 180^{\circ}-50^{\circ}=130^{\circ}$。
【答案】：$\angle3 = 70^{\circ}$，$\angle4 = 130^{\circ}$