《2025年实验班提优训练暑假衔接版二生三年级数学人教版》

例2 说一说,猜一猜。

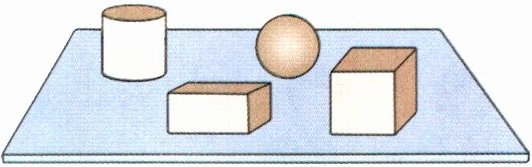
我观察一个立体图形,看到的一个面是正方形。
可能是正方体,因为正方体的面都是正方形。也可能是……

答案： 过程探索
(1)正方体所有的面都是()形,所以可能是正方体。
(2)长方体左、右两个面可能是正方形,所以可能是()。
(3)从正面或侧面观察此类圆柱,所看到的形状也是正方形,所以也可能是()。
完全解答 这个立体图形可能是正方体,也可能是长方体,还可能是圆柱。

例3 把长方体纸盒剪开,平铺在桌面上。(注意:每个面都至少有一条边和其他的面相连)
(1)需要剪开几条边?想一想,描一描。
(2)剪一剪,说一说。
(3)你能在剪开后的图形上找到原来纸盒上的6个面吗?想一想,说一说。

答案：
过程探索
盒,只需要剪开连接两个口的一
(1)如图①,开了两个口的长方体纸
上面开了一个口,只需要剪开四条边(侧面一条,底部三条)。如图③,这个纸盒没有开口,需要剪开七条边才能完全展开。因为需要确保每个面都能展开,并且每个面至少有一条边和其他面相连。

(2)纸盒的每个面都是成对出现的,每对中的两个面在纸盒上是相对的,但在展开的图形中是不相连的。即使是同一个纸盒,如果选择剪开不同的边,最终得到的展开图形也会有所不同。
(3)①确定“前面”:首先,确定展开图形中哪个面是“前面”。这通常可
完全解答 见过程探索。