《2025年巅峰对决八年级数学上册人教版》

1.在△ABC 中,∠A= 20°,∠B= 4∠C,则∠C 的度数为 (A)
A.32°
B.36°
C.40°
D.128°

答案： 解：在△ABC中，∠A+∠B+∠C=180°。
∵∠A=20°，∠B=4∠C，
∴20°+4∠C+∠C=180°，
5∠C=160°，
∠C=32°。
答案：A

2.如图,已知l//AB,CD⊥l于点 D.若∠C= 40°,则∠1 的度数是 (C)
A.30°
B.40°
C.50°
D.60°

答案： 解：
∵CD⊥l，
∴∠CDD'=90°（设l与BC交于点D'）。
在△CDD'中，∠C=40°，∠CDD'=90°，
∴∠CD'D=180°-∠C-∠CDD'=180°-40°-90°=50°。
∵l//AB，
∴∠1=∠CD'D=50°（两直线平行，同位角相等）。
答案：C

3.在△ABC 中,若一个内角等于另外两个内角的差,则 (D)
A.必有一个内角等于 30°
B.必有一个内角等于 45°
C.必有一个内角等于 60°
D.必有一个内角等于 90°

答案： 解：设△ABC的三个内角分别为∠A、∠B、∠C，且∠A = ∠B - ∠C（∠B ＞ ∠C）。
∵∠A + ∠B + ∠C = 180°（三角形内角和定理），
又∠A = ∠B - ∠C，
∴∠B - ∠C + ∠B + ∠C = 180°，
∴2∠B = 180°，
∴∠B = 90°。
同理，若∠B = ∠A - ∠C或∠C = ∠A - ∠B，可证得其他角为90°。
结论：必有一个内角等于90°。
D

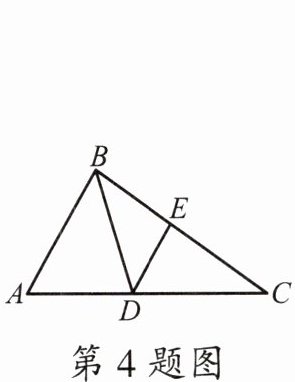
4.如图,在△ABC 中,∠A= 70°,∠C= 30°,BD 平分∠ABC 交 AC 于点 D,DE//AB,交 BC 于点 E,则∠BDE 的度数是 (B)

A.30°
B.40°
C.50°
D.60°

答案： 解：在△ABC中，∠A=70°，∠C=30°，
∠ABC=180°-∠A-∠C=180°-70°-30°=80°.
∵BD平分∠ABC，
∴∠ABD=∠ABC/2=80°/2=40°.
∵DE//AB，
∴∠BDE=∠ABD=40°.
答案：B

5.(2024·南开中学七下期中)如图,D 为△ABC 边 AB 上一点,M,N 为边 AC,BC 上的点,将△ADM,△BDN 分别沿着 DM,DN 翻折,得到△A'DM 和△B'DN.若 MA'//NB',设∠C= α,则∠MDN 的度数是 (C)
A.$180^{\circ }-\frac {1}{2}\alpha$
B.$180^{\circ }-\alpha$
C.$90^{\circ }+\frac {1}{2}\alpha$
D.$90^{\circ }+\alpha$

答案： 解：设∠ADM=∠A'DM=x，∠BDN=∠B'DN=y，
则∠MDN=180°-x-y，∠A=∠A'，∠B=∠B'。
∵MA'//NB'，
∴∠A'+∠B'=180°，即∠A+∠B=180°。
在△ABC中，∠A+∠B=180°-∠C=180°-α，
∴∠A'+∠B'=180°-α。
在△A'DM中，∠A'DM+∠A'+∠A'MD=180°，
同理∠B'DN+∠B'+∠B'ND=180°，
∵∠A'MD=∠AMD，∠B'ND=∠BND，
∠AMD+∠DMC=180°，∠BND+∠DNC=180°，
又∠DMC+∠DNC+∠C+∠MDN=360°，
即(180°-∠AMD)+(180°-∠BND)+α+(180°-x-y)=360°，
整理得(180°-(180°-x-∠A'))+(180°-(180°-y-∠B'))+α+180°-x-y=360°，
化简得x+∠A'+y+∠B'+α+180°-x-y=360°，
即∠A'+∠B'+α+180°=360°，
∵∠A'+∠B'=180°-α，
∴180°-α+α+180°=360°，恒成立。
在△ADM中，∠A=180°-2x-∠AMD，
同理∠B=180°-2y-∠BND，
∠A+∠B=360°-2(x+y)-(∠AMD+∠BND)=180°-α，
又∠AMD+∠BND=360°-α-(180°-x-y)=180°-α+x+y，
代入得360°-2(x+y)-(180°-α+x+y)=180°-α，
解得x+y=90°-$\frac{1}{2}$α，
∴∠MDN=180°-(x+y)=180°-(90°-$\frac{1}{2}$α)=90°+$\frac{1}{2}$α。
答案：C

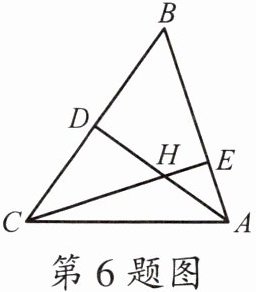
6.如图,在△ABC 中,△ABC 的高 AD,CE 相交于点 H,∠B= 57°,则∠AHC 的度数是______.

123°

答案： 解：
∵AD，CE是△ABC的高，
∴∠ADB=∠CEB=90°．
在△ABD中，∠BAD=180°-∠ADB-∠B=180°-90°-57°=33°．
在△AHE中，∠AEH=90°，
∴∠AHC=∠EAH+∠AEH=33°+90°=123°．
123°

7.如图,在△ABC 中,∠1= ∠2,∠BAC= 65°,则∠APB 的度数是______.

130°

答案： 解：在△ABC中，∠BAC=65°，
∴∠ABC+∠ACB=180°-∠BAC=115°.
∵∠1=∠2，
∴∠PBC+∠PCB=∠ABC+∠ACB-（∠1+∠2）=115°-（∠1+∠2）.
又
∵∠1+∠2=∠BAC=65°，
∴∠PBC+∠PCB=115°-65°=50°.
在△PBC中，∠APB=180°-（∠PBC+∠PCB）=180°-50°=130°.
130°

8.在△ABC 中,三个内角∠A,∠B,∠C 分别满足下列条件,请求出∠B 的度数.
(1)若∠B-∠A= ∠C-∠B,则∠B= 60度；
(2)若∠A= 2∠B= 3∠C,则∠B= 540/11度；
(3)若∠A+∠C= ∠B,则∠B= 90度；
(4)若∠A= $\frac {1}{2}$∠B= $\frac {1}{3}$∠C,则∠B= 60度；

答案：
(1)解：
∵∠B-∠A=∠C-∠B
∴2∠B=∠A+∠C
∵在△ABC中，∠A+∠B+∠C=180°
∴∠A+∠C=180°-∠B
∴2∠B=180°-∠B
3∠B=180°
∠B=60°
(2)解：设∠A=6x，则∠B=3x，∠C=2x（设∠A=6x，使∠B、∠C系数为整数）
∵∠A+∠B+∠C=180°
∴6x+3x+2x=180°
11x=180°
x=180°/11
∠B=3x=540°/11≈49.09°（按题目要求保留分数形式）
∠B=540/11
(3)解：
∵∠A+∠C=∠B，且∠A+∠B+∠C=180°
∴∠B+∠B=180°
2∠B=180°
∠B=90°
(4)解：设∠A=x，则∠B=2x，∠C=3x
∵∠A+∠B+∠C=180°
∴x+2x+3x=180°
6x=180°
x=30°
∠B=2x=60°
答案：
(1)60；
(2)540/11；
(3)90；
(4)60

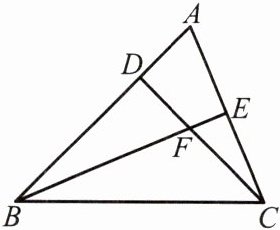
9.如图,在△ABC 中,已知∠ACB= 67°,BE 是 AC 上的高,CD 是 AB 上的高,F 是 BE 和 CD 的交点,∠DCB= 45°,求∠ABE 和∠BFC 的度数.

答案： 解：
∵CD是AB上的高，
∴∠BDC=90°，
在△BDC中，∠DBC=180°-∠BDC-∠DCB=180°-90°-45°=45°，
∵∠ACB=67°，∠DCB=45°，
∴∠ACD=∠ACB-∠DCB=67°-45°=22°，
∵BE是AC上的高，
∴∠BEC=90°，
在△CEF中，∠EFC=180°-∠BEC-∠ACD=180°-90°-22°=68°，
∴∠BFC=180°-∠EFC=180°-68°=112°，
∵∠AEB=90°，∠A+∠ABE=90°，∠A+∠ACD=90°，
∴∠ABE=∠ACD=22°．
答：∠ABE=22°，∠BFC=112°．