《2025年巅峰对决八年级数学上册人教版》

1.将一副三角板按如图所示的方式重叠,则∠1的度数为 (C)
A.45°
B.60°
C.75°
D.105°

答案： 解：由图可知，一副三角板中，一个三角板的锐角为45°，另一个三角板的锐角为30°。∠1是这两个三角板重叠后形成的三角形的一个外角，根据三角形外角等于不相邻两个内角之和，可得∠1=45°+30°=75°。
答案：C

2.一副三角板按如图所示的方式摆放,若∠1= 80°,则∠2的度数为 (D)
A.80°
B.95°
C.100°
D.110°

答案： 解：由图可知，含30°角的直角三角板中，另一个锐角为60°；含45°角的直角三角板中，两个锐角均为45°。
设∠1的邻补角为∠3，则∠3=180°-∠1=180°-80°=100°。
在三角形中，∠3为一个外角，等于与它不相邻的两个内角之和，即∠3=30°+∠4（∠4为含45°角三角板中与∠2相关的内角），则∠4=∠3-30°=100°-30°=70°。
∠2与∠4互补（平角定义），所以∠2=180°-∠4=180°-70°=110°。
答案：D

3.如图,在△CEF中,∠E= 80°,∠F= 50°,AB//CF,AD//CE,连接BC,CD,则∠A的度数是 (B)
A.45°
B.50°
C.55°
D.80°

答案： 解：在△CEF中，∠E=80°，∠F=50°，
∠ECF=180°-∠E-∠F=180°-80°-50°=50°.
∵AB//CF，
∴∠ABC=∠BCF（两直线平行，内错角相等）.
∵AD//CE，
∴∠ADC=∠DCE（两直线平行，内错角相等）.
在四边形ABCD中，∠A+∠ABC+∠BCD+∠ADC=360°.
∵∠BCD=∠BCF+∠ECF+∠DCE，
∴∠A+∠BCF+∠BCF+∠ECF+∠DCE+∠DCE=360°，
即∠A+2(∠BCF+∠DCE)+∠ECF=360°.
又
∵∠ABC+∠ADC=∠BCF+∠DCE，
设∠BCF+∠DCE=x，则∠A+2x+50°=360°，∠A=310°-2x.
在△ABC和△ADC中，无法直接得出更多关系，考虑延长BC交AD于点G.
∵AD//CE，
∴∠BGD=∠BCE（两直线平行，同位角相等）.
∵AB//CF，
∴∠ABG=∠BCF（已证）.
∠BCE=∠BCF+∠ECF=∠ABG+50°.
∠AGB=180°-∠BGD=180°-(∠ABG+50°)=130°-∠ABG.
在△ABG中，∠A+∠ABG+∠AGB=180°，
∠A+∠ABG+130°-∠ABG=180°，
∠A=50°.
答案：B.

4.如图,在△ABC中,∠A= 60°,∠B= 70°,CD是∠ACB的平分线,CH⊥AB于点H,则∠DCH的度数为 (A)
A.5°
B.10°
C.15°
D.20°

答案： 解：在△ABC中，∠A=60°，∠B=70°，
∠ACB=180°-∠A-∠B=180°-60°-70°=50°.
∵CD是∠ACB的平分线，
∴∠ACD=∠BCD=∠ACB/2=50°/2=25°.
在△BCH中，CH⊥AB，∠B=70°，
∠BCH=90°-∠B=90°-70°=20°.
∠DCH=∠BCD-∠BCH=25°-20°=5°.
答案：A.

5.把△ABC沿EF对折,折叠后的图形如图所示.若∠A= 60°,∠1= 96°,则∠2的度数为 (B)
A.30°
B.24°
C.25°
D.26°

答案： 解：在△ABC中，∠A=60°，
∴∠AEF+∠AFE=180°-∠A=120°.
∵∠AEF+∠B'EF+∠1=180°，∠AFE+∠C'FE+∠2=180°，
由折叠性质得∠AEF=∠B'EF，∠AFE=∠C'FE，
∴2∠AEF+∠1=180°，2∠AFE+∠2=180°.
两式相加：2(∠AEF+∠AFE)+∠1+∠2=360°，
即2×120°+96°+∠2=360°，
解得∠2=24°.
答案：B

6.某机器零件的横截面如图所示,按要求线段AB和DC的延长线相交成直角才算合格.一工人测得∠A= 23°,∠D= 31°,∠AED= 143°,请你帮他判断该零件是否合格:不合格. (填“合格”或“不合格”)

答案： 【解析】：
根据三角形的外角性质，我们可以知道，$\angle AED$应该等于$\angle D+\angle ECD$，同时也应该等于$\angle A+\angle B+\angle D$（将$ \angle BEC$看作$ \angle A$与$ \angle B$的外角），由此可求出$\angle ECD$或者$\angle B$的度数，看是否满足相交成直角的要求。
【答案】：
解：
延长$AB$、$DC$相交于点$F$。
因为$\angle AED=\angle A+\angle D+\angle F$，
$\angle A=23^\circ$，$\angle D=31^\circ$，$\angle AED=143^\circ$，
所以$\angle F=143^\circ-23^\circ-31^\circ=89^\circ\neq 90^\circ$，
因为$\angle F$不是直角，
所以$AB$与$DC$的延长线相交不成直角，
所以该零件不合格。
故答案为不合格。

7.国旗上的一个五角星如图所示,则∠A+∠B+∠C+∠D+∠E= ______度.

180

答案： 【解析】：本题可根据三角形外角的性质，将$\angle A$、$\angle B$、$\angle C$、$\angle D$、$\angle E$这五个角的和转化为与三角形内角和相关的形式来求解。
设$BC$与$AD$相交于点$F$，$BC$与$AE$相交于点$G$。
根据三角形外角的性质：三角形的一个外角等于与它不相邻的两个内角之和。
在$\triangle FDG$中，$\angle DFG$是外角，则$\angle DFG = \angle D + \angle E$；
在$\triangle FCG$中，$\angle CGF$是外角，则$\angle CGF = \angle C + \angle B$。
而在$\triangle AFG$中，$\angle A + \angle DFG + \angle CGF = 180^{\circ}$（三角形内角和为$180^{\circ}$）。
把$\angle DFG = \angle D + \angle E$，$\angle CGF = \angle C + \angle B$代入$\angle A + \angle DFG + \angle CGF = 180^{\circ}$可得：
$\angle A + (\angle D + \angle E)+(\angle C + \angle B)= 180^{\circ}$，即$\angle A + \angle B + \angle C + \angle D + \angle E = 180^{\circ}$。
【答案】：$180$

8.如图是可调躺椅示意图(数据如图),AE与BD的交点为点C,且∠CAB,∠CBA,∠E保持不变.为了舒适,需调整∠D的大小,使∠EFD= 110°,则图中∠D应减少(填“增加”或“减少”)40度.

答案： 解：在△ABC中，∠ACB=180°-∠CAB-∠CBA=180°-50°-60°=70°，
∴∠ECD=∠ACB=70°。
在△CDE中，∠DCE+∠E+∠CDE=180°，
∴∠CDE=180°-∠DCE-∠E=180°-70°-30°=80°，即∠EDF=80°。
在△DEF中，∠EFD=110°，∠E=30°，
∴∠EDF'=180°-∠EFD-∠E=180°-110°-30°=40°。
∵∠EDF'=40°，∠EDF=80°，
∴∠D应减少80°-40°=40度。
减少；40

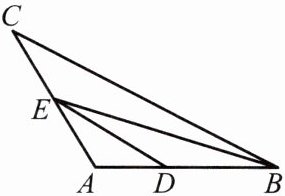
9.如图,BE是△ABC的角平分线,DE//BC,交AB于点D,∠A= 126°,∠DEB= 14°,求∠BEC的度数.

答案： 解：
∵DE//BC，
∴∠DEB=∠EBC=14°（两直线平行，内错角相等）。
∵BE是△ABC的角平分线，
∴∠ABC=2∠EBC=2×14°=28°。
在△ABC中，∠A=126°，∠ABC=28°，
∴∠C=180°-∠A-∠ABC=180°-126°-28°=26°。
在△BEC中，∠BEC=180°-∠EBC-∠C=180°-14°-26°=140°。