《2025年全频道课时作业四年级数学下册人教版》

3. 把下面三角形的序号填在相应的框里。
　

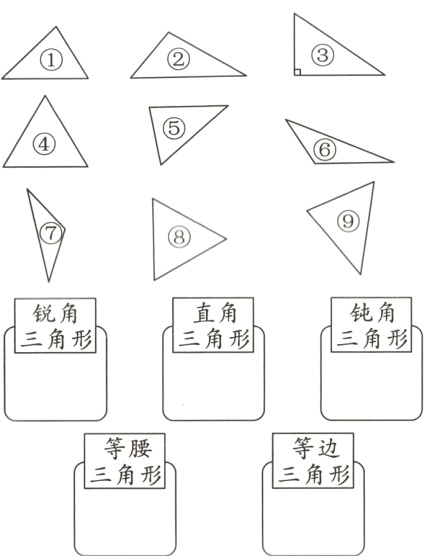
答案： ①④⑤⑧⑨ ③ ②⑥⑦ ④⑦⑧ ④⑧

4. 在下面的点子图上画一个直角三角形和一个既是等腰三角形，又是钝角三角形的三角形。
　

答案： 略

5. 求下面各图中未知角的度数。

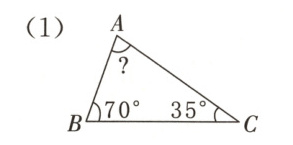
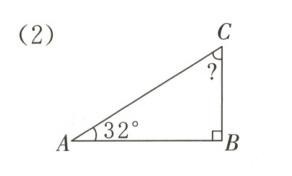
答案：
(1)$\angle A = 180^{\circ}-70^{\circ}-35^{\circ}=75^{\circ}$
(2)$\angle C = 180^{\circ}-90^{\circ}-32^{\circ}=58^{\circ}$

6. [思维拓展]有一堆碎纸片（如下图），浩浩认为一定能从中挑出3张纸片，使它们对应的三个角凑在一起能拼成一个等腰三角形，你同意他的想法吗？写出你的理由。
　

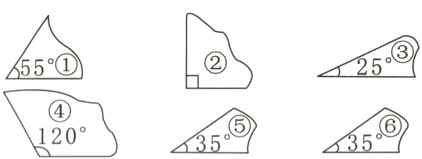
答案： 不同意。理由：等腰三角形有两个底角相等，可以选纸片⑤和⑥，根据三角形的内角和为$180^{\circ}$，可知第三个内角为$180^{\circ}-35^{\circ}-35^{\circ}=110^{\circ}$，纸片里面没有角度为$110^{\circ}$的，所以不能拼成等腰三角形。

7. [推理探究]如图所示，三角形ABC为等边三角形，∠1 = ∠2，求∠3的度数。（写出求解过程）
　　　　　　　　　　　

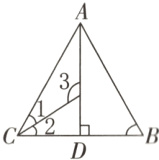
答案： 因为三角形 ABC 为等边三角形
所以$\angle BAC=\angle BCA=\angle ABC = 60^{\circ}$
因为$\angle 1+\angle 2=\angle BCA = 60^{\circ}$，且$\angle 1=\angle 2$
所以$\angle 1 = 30^{\circ}$
因为$\angle ADC = 90^{\circ}$
即$\angle DAC = 180^{\circ}-\angle BCA-\angle ADC = 180^{\circ}-60^{\circ}-90^{\circ}=30^{\circ}$
故$\angle 3 = 180^{\circ}-30^{\circ}-30^{\circ}=120^{\circ}$