《2025年全频道课时作业四年级数学下册人教版》

1. 填空。
（1）一个三角形的两个内角分别是24°和88°，另一个角是(　　　)，这是一个(　　　)三角形。
（2）一个直角三角形的一个锐角是65°，另一个锐角是(　　　)。
（3）任意一个四边形的内角中最多有(　　　)个直角，最多有(　　　)个钝角，最多有(　　　)个锐角。

答案：
(1)$68^{\circ}$ 锐角
(2)$25^{\circ}$
(3)4 3 3

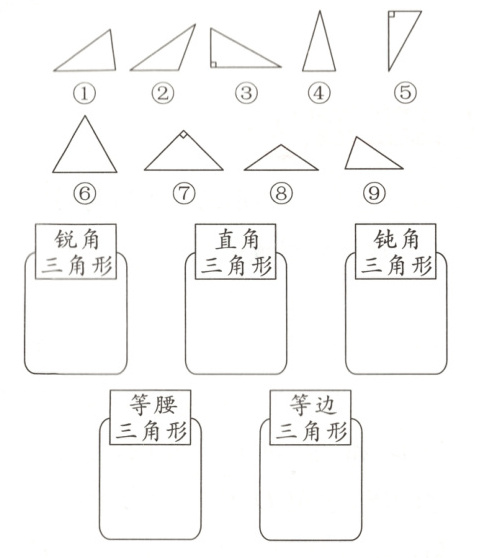
2. 把下面三角形的序号填在相应的圈里。

答案： 锐角三角形：①④⑥⑨
直角三角形：③⑤⑦
钝角三角形：②⑧
等腰三角形：②④⑥⑦⑧
等边三角形：⑥

3. 画一个三角形，使它既是直角三角形，又是等腰三角形，并画出斜边上的高。

答案： 略

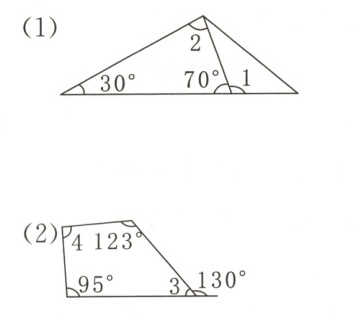
4. 计算下面图形中∠1，∠2，∠3，∠4的度数。

答案：
(1)$\angle1 = 180^{\circ}-70^{\circ}=110^{\circ}$ $\angle2 = 180^{\circ}-30^{\circ}-70^{\circ}=80^{\circ}$
(2)$\angle3 = 180^{\circ}-130^{\circ}=50^{\circ}$
$\angle4 = 360^{\circ}-123^{\circ}-95^{\circ}-50^{\circ}=92^{\circ}$

5. “又是一年三月三，风筝飞满天”，放风筝是民间传统游戏之一。可可做了一个等腰三角形形状的风筝。如果等腰三角形的两条边长分别是46 cm和21 cm，这个等腰三角形的周长是多少厘米？

答案： $46 + 21 + 46 = 113(\text{cm})$
[解析]根据三角形两边和应大于第三边，确定等腰三角形第三边的长度。等腰三角形两边分别是46 cm和21 cm，那么第三条边的长度应该是46 cm，因为$21 + 21 = 42(\text{cm})$，$42＜46$(不能组成三角形)。$46 + 21 = 67(\text{cm})$，$67＞46$(能组成三角形)，所以周长是$46 + 21 + 46 = 113(\text{cm})$。

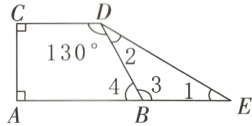
6. 如图，已知BD=BE，求∠1的度数。
　　　　　　　　

答案： $\angle4 = 360^{\circ}-90^{\circ}-90^{\circ}-130^{\circ}=50^{\circ}$
$\angle3 = 180^{\circ}-50^{\circ}=130^{\circ}$
$\angle1=(180^{\circ}-130^{\circ})\div2 = 25^{\circ}$