第63页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
1. 填空。
(1)一个正方体魔方的表面积是 54 平方厘米,则其一个面的面积是( )平方厘米。
(2)一个正方体的棱长总和是 72 厘米,它的一个面是边长为( )厘米的正方形,它的表面积是( )平方厘米。
(3)若正方体的棱长扩大到原来的 2 倍,则其表面积扩大到原来的( )倍。
(4)用 4 个棱长为 3 厘米的正方体拼成一个长方体,表面积最多减少( )平方厘米。
(1)一个正方体魔方的表面积是 54 平方厘米,则其一个面的面积是( )平方厘米。
(2)一个正方体的棱长总和是 72 厘米,它的一个面是边长为( )厘米的正方形,它的表面积是( )平方厘米。
(3)若正方体的棱长扩大到原来的 2 倍,则其表面积扩大到原来的( )倍。
(4)用 4 个棱长为 3 厘米的正方体拼成一个长方体,表面积最多减少( )平方厘米。
答案:
9@@6@@216@@4@@72
2. 一个棱长 5 cm 的正方体罐头盒,在盒子的 4 个侧面贴上商标纸。这张商标纸的面积至少应有多少平方分米?
答案:
$5×5×4 = 100(cm^{2})$
$100 cm^{2}=1 dm^{2}$
答:这张商标纸的面积至少应有$1 dm^{2}$。
3. [教材改编]一个通风管(如下图)长 3 米,它的横截面是边长为 0.5 米的正方形,如果用铁皮做这样的通风管 50 个,需要多少平方米的铁皮?


答案:
$0.5×3×4 = 6$(平方米)
$6×50 = 300$(平方米)
答:需要300平方米的铁皮。
4. 一个长方体(如图),如果高增加 2 厘米,就变成了棱长是 10 厘米的正方体,长方体的表面积增加了多少?
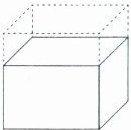

答案:
$10×2×4 = 80$(平方厘米)
答:长方体的表面积增加了80平方厘米。
5. 有两个相同的长方体糖果盒,长、宽、高分别是 10 cm、6 cm、2 cm,用包装纸将它们全封闭包装在一起,拼成一个新的长方体。
(1)请你设计出三种方案,写出所拼成的长方体的长、宽、高,并计算出每种方案拼成的长方体的表面积。
| | 长(cm) | 宽(cm) | 高(cm) | 表面积(cm²) |
| ---- | ---- | ---- | ---- | ---- |
| 方案一 | | | | |
| 方案二 | | | | |
| 方案三 | | | | |
(2)哪种方案最省包装纸? 你发现了什么?
(1)请你设计出三种方案,写出所拼成的长方体的长、宽、高,并计算出每种方案拼成的长方体的表面积。
| | 长(cm) | 宽(cm) | 高(cm) | 表面积(cm²) |
| ---- | ---- | ---- | ---- | ---- |
| 方案一 | | | | |
| 方案二 | | | | |
| 方案三 | | | | |
(2)哪种方案最省包装纸? 你发现了什么?
答案:
20@@6@@2@@344@@10@@6@@4@@248@@12@@10@@2@@328@@拼成长10 cm、宽6 cm、高4 cm的长方体最省包装纸。发现:两个小长方体重合的面积越大,拼成的大长方体表面积越小。(发现不唯一,合理即可)
解析:对应的三种方案分别是左右面重合、上下面重合和前后面重合。
查看更多完整答案,请扫码查看


