《2025年小学学霸作业本五年级数学下册青岛版山东专版》

1. [新趋势·算理探究]求12和30的最大公因数。

答案： 1,2,3,4,6,12@@1,2,3,5,6,10,15,30@@1,2,3,6@@6@@3@@2@@5@@2@@3@@6

2. 在下面的圈里填上合适的数,并填空。

18和32的最大公因数是(  )。                                            36和24的最大公因数是( )。

答案：
@@@@2@@12

3. 判断。
(1)两个数的最大公因数一定小于这两个数。 ( )
(2)每个数的因数个数有限,因此两个数的公因数个数也有限。 ( )
(3)两个质数的最大公因数是1。 ( )
(4)任意两个偶数(0除外)的公因数一定都有2。 ( )

答案： ×@@√@@√@@√

4. 用短除法找出每组数的最大公因数。
8和12
42和63
84和36
34和51

答案：

$8和12的最大公因数是:2\times2 = 4。 42和63的最大公因数是:3\times7 = 21。84和36的最大公因数是:2\times2\times3 = 12。 34和51的最大公因数是17。$

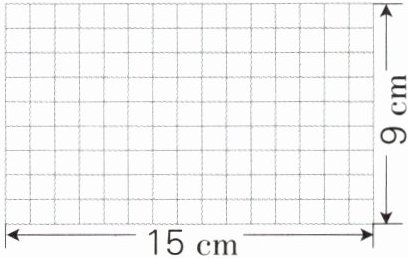
5. [新趋势·思维探究]如图,把一张长15厘米、宽9厘米的长方形纸裁成同样大的正方形(边长是整厘米数)且纸没有剩余,裁出的正方形边长可以是( )厘米,这是求15和9的( );裁出的正方形边长最大是( )厘米,这是求15和9的( ),一共可以裁出( )个这样的正方形。(先在图中画一画,再回答)

答案： 1或3@@公因数@@3@@最大公因数@@15@@解析: 裁成同样大小，且没有剩余，就是裁成的小正方形的边长是15和9的公因数，要求面积最大的正方形，就是以15和9的最大公因数为小正方形的边长，然后用长方形纸的长和宽分别除以小正方形的边长，就是长方形纸的长边可以裁几个，宽边可以裁几个，最后把它们乘起来即可。