《2025年亮点给力提优课时作业本九年级物理下册苏科版》

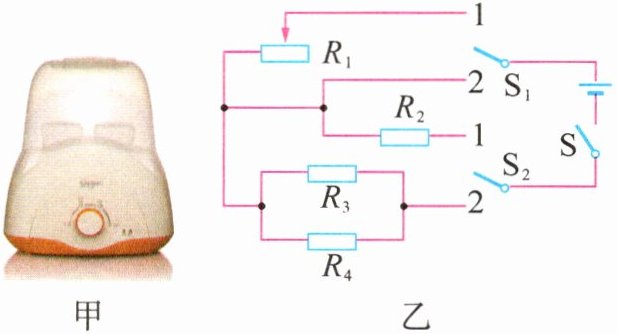
4. （2024·湖北武汉模拟）如图甲所示是一款暖奶器，它可以实现高温定挡消毒、中温定挡加热和低温可调保温三种功能，其电路结构如图乙所示。暖奶器的电源电压保持$40\ V$不变，发热电阻$R_2$、$R_3$和$R_4$分别为$10\ \Omega$、$5\ \Omega$和$40\ \Omega$，$R_1$是规格为“$30\ \Omega\ \ 2\ A$”的滑动变阻器。$S$闭合，$S_1$、$S_2$均接$1$时，暖奶器处于低温挡，移动滑片，可以手动调节低温挡的保温功率。下列说法正确的是 （ ）
①$S$闭合，$S_1$、$S_2$均接$2$时，暖奶器有高温定挡消毒功能
②暖奶器以中温挡工作时，发热电阻$5\ min$产生的热量为$800\ J$
③暖奶器以低温挡工作时，保温功率最大为$80\ W$
④暖奶器以低温挡工作时，保温功率最小为$10\ W$

A. ①③
B. ①④
C. ②③
D. ②④

答案： A@@解析：由图乙可知，$S$闭合，$S_{1}$、$S_{2}$均接1时，滑动变阻器$R_{1}$和定值电阻$R_{2}$串联，总电阻最大，由$P=\frac{U^{2}}{R}$可知，总功率最小，暖奶器处于低温挡，可通过变阻器$R_{1}$调节保温功率；$S$闭合，$S_{1}$、$S_{2}$均接2时，$R_{3}$和$R_{4}$并联，总电阻最小，总功率最大，暖奶器处于高温挡，有定挡消毒功能；$S$闭合，$S_{1}$接2、$S_{2}$接1时，只有电阻$R_{2}$工作，电阻较大，暖奶器处于中温挡。 ① 由以上分析可知，$S$闭合，$S_{1}$、$S_{2}$均接2时，暖奶器有高温定挡消毒功能，故①正确； ② 暖奶器中温挡时，只有电阻$R_{2}$工作，发热电阻5 min产生的热量$Q = W=\frac{U^{2}}{R_{2}}t=\frac{(40V)^{2}}{10\Omega}×5×60s = 48000J$，故②错误； ③ 暖奶器以低温挡工作时，若滑片移至最左端，$R_{1}$接入阻值为零，电路中电流$I=\frac{U}{R_{2}}=\frac{40V}{10\Omega}=4A$，超过滑动变阻器允许的最大电流$2A$，所以电路的最大电流为$2A$，保温功率最大为$P_{大}=UI_{大}=40V×2A = 80W$，故③正确； ④ 低温挡工作时，滑片移至最右端，$R_{1}$接入阻值最大，电路电流最小，保温功率最小，最小功率$P_{小}=\frac{U^{2}}{R_{1大}+R_{2}}=\frac{(40V)^{2}}{30\Omega + 10\Omega}=40W$，故④错误。综上所述，A正确。

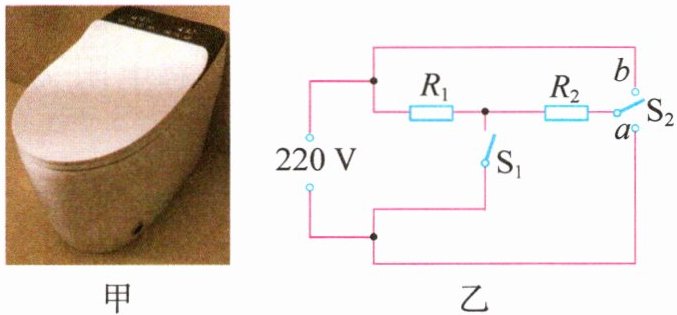
5. 如图甲为家用智能电热马桶盖，图乙是其电路原理图，$R_1$和$R_2$是两个定值电阻（表示两个电热丝），单刀双掷开关$S_2$可接$a$或$b$，该电路通过开关$S_1$和$S_2$的不同接法组合，实现“高温挡、中温挡、低温挡”三种加热功能。当开关$S_1$断开、$S_2$接$a$时，电路的功率为$44\ W$；开关$S_1$闭合、$S_2$接$a$时，电路的功率为$88\ W$。求：
（1）$R_2$的阻值。
（2）开关$S_1$闭合、$S_2$接$b$时，电路的功率。
（3）马桶圈的质量$m = 650\ g$，要让马桶圈的温度升高$8\ ^{\circ}C$，用“高温挡”加热的方式需要的时间。[设电热丝产生的热量全部被马桶圈吸收，马桶圈材料的比热容$c = 0.44×10^3\ J/(kg·^{\circ}C)$]

答案：
(1) $550\Omega$
(2) $176W$
(3) $13s$ 解析：
(1) 由图乙可知，当开关$S_{1}$闭合、$S_{2}$接$a$时，电路为$R_{1}$的简单电路，此时$P_{2}=88W$，则$R_{1}$的阻值$R_{1}=\frac{U^{2}}{P_{2}}=\frac{(220V)^{2}}{88W}=550\Omega$，当开关$S_{1}$断开、$S_{2}$接$a$时，$R_{1}$和$R_{2}$串联，此时$P_{1}=44W$，电路中的总电阻$R=\frac{U^{2}}{P_{1}}=\frac{(220V)^{2}}{44W}=1100\Omega$，所以$R_{2}$的阻值$R_{2}=R - R_{1}=1100\Omega - 550\Omega = 550\Omega$。
(2) 由图乙可知，当开关$S_{1}$闭合、$S_{2}$接$b$时，$R_{1}$与$R_{2}$并联，电路的功率$P_{3}=P_{R1}+P_{R2}=\frac{U^{2}}{R_{1}}+\frac{U^{2}}{R_{2}}=\frac{(220V)^{2}}{550\Omega}+\frac{(220V)^{2}}{550\Omega}=176W$。
(3) 马桶圈吸收的热量$Q_{吸}=cm\Delta t = 0.44×10^{3}J/(kg\cdot^{\circ}C)×650×10^{-3}kg×8^{\circ}C = 2288J$，由以上分析可知，“高温挡”加热功率$P_{高温}=P_{3}=176W$，电热丝产生的热量全部被马桶圈吸收，则电热丝消耗的电能$W = Q_{吸}=2288J$，用“高温挡”加热的方式需要的时间$t=\frac{W}{P_{高温}}=\frac{2288J}{176W}=13s$。

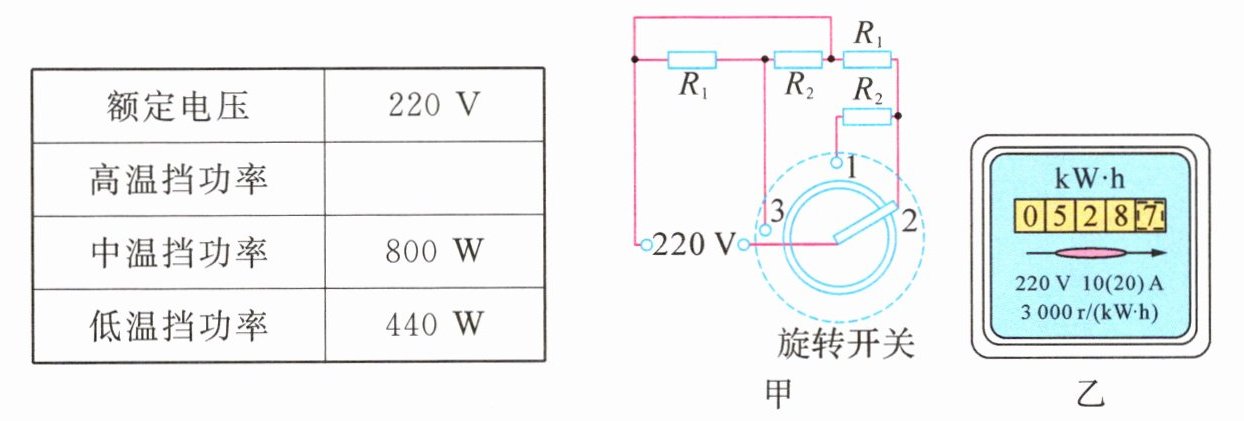
6. （2024·山东东营一模）随着生活质量的提升，各类空气炸锅、电烤箱、烧烤炉走进了千家万户，小明家新买了一个三挡位的电烤箱，电烤箱的相关参数如表所示，小明研究电烤箱加热板部分，画出了其简化电路如图甲所示，$R_1$、$R_2$是定值电阻，可通过旋转开关实现高、中、低挡位切换。则：

（1）电烤箱在低温挡正常工作时的电流是多少？
（2）电烤箱中$R_2$的阻值是多少？
（3）若在用电高峰期，家庭电路的实际电压会降低，电烤箱在中温挡工作$3\ min$能使图乙中的电能表（不受电压影响）转盘转动$105$圈，则此段时间中温挡实际电功率是多少？
（4）电烤箱在中温挡正常工作$2\ min$，它能将质量为$1\ kg$、初温为$20\ ^{\circ}C$的蛋糕液加热到多少摄氏度？[不计热量损失，蛋糕液的比热容取$2.2×10^3\ J/(kg·^{\circ}C)$]

答案：
(1) $2A$
(2) $49.5\Omega$
(3) $700W$
(4) $63.6^{\circ}C$ 解析：
(1) 由表格数据可知，电烤箱低温挡的功率$P_{低温}=440W$，由$P = UI$可得，电烤箱在低温挡正常工作时的电流$I_{低温}=\frac{P_{低温}}{U}=\frac{440W}{220V}=2A$。
(2) 由图甲可知，当旋转开关接1时，$R_{1}$、$R_{2}$串联，此时电路的总电阻最大，由$P=\frac{U^{2}}{R}$可知，总功率最小，电烤箱处于低温挡；当旋转开关接3时，$R_{1}$、$R_{2}$并联，此时电路的总电阻最小，总功率最大，电烤箱处于高温挡；当旋转开关接2时，只有$R_{1}$工作，电烤箱处于中温挡。由$P=\frac{U^{2}}{R}$可得，$R_{1}$的阻值$R_{1}=\frac{U^{2}}{P_{中温}}=\frac{(220V)^{2}}{800W}=60.5\Omega$，$R_{1}$、$R_{2}$串联的总电阻$R=\frac{U^{2}}{P_{低温}}=\frac{(220V)^{2}}{440W}=110\Omega$，$R_{2}$的阻值$R_{2}=R - R_{1}=110\Omega - 60.5\Omega = 49.5\Omega$。
(3) 图乙中的$3000r/(kW\cdot h)$表示电路中的用电器每消耗$1kW\cdot h$电能，电能表的转盘转过3000圈，则电能表的转盘转过105圈，此过程中电烤箱消耗的电能$W=\frac{105r}{3000r/(kW\cdot h)}=0.035kW\cdot h = 1.26×10^{5}J$，此段时间中温挡实际电功率$P_{实}=\frac{W}{t'}=\frac{1.26×10^{5}J}{3×60s}=700W$。
(4) 电烤箱中温挡工作2 min消耗的电能$W' = P_{中温}t'' = 800W×2×60s = 9.6×10^{4}J$，不计热量损失，蛋糕液吸收的热量$Q_{吸}=W' = 9.6×10^{4}J$，由$Q_{吸}=cm(t - t_{0})$可得，蛋糕液的末温$t=\frac{Q_{吸}}{cm}+t_{0}=\frac{9.6×10^{4}J}{2.2×10^{3}J/(kg\cdot^{\circ}C)×1kg}+20^{\circ}C\approx63.6^{\circ}C$。