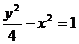24.(薛中)已知定点A(3,0),B(0,3)如果线段AB与抛物线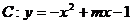 有且仅有一个公共点,试求m的取值范围。
有且仅有一个公共点,试求m的取值范围。
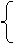 答案:设线段AB上任意一点
答案:设线段AB上任意一点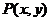 ,可看作线段AB的定比分点,所以
,可看作线段AB的定比分点,所以 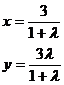
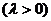 ,由线段AB与抛物线C有且仅有一个公共点,所以方程
,由线段AB与抛物线C有且仅有一个公共点,所以方程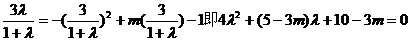 有且仅有一个正根,所以
有且仅有一个正根,所以 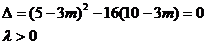 1或
1或 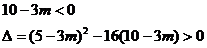 2
2
解1得m=3, 解2得m>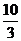 ,综上所述m>
,综上所述m>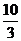 或m=3。
或m=3。
错解:直线AB的方程为y=-x+3,因为AB与抛物线C有且仅有一个公共点,所以方程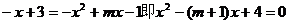 的判别
的判别
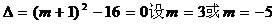 。
。
错因:审题不严,显现条件弱用,把求线段AB与抛物线C的交点变成了求直线AB与抛物线C的交点。
23.(薛中)直线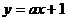 与双曲线
与双曲线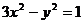 相交于点A,B,是否存在这样的实数a,使得A,B关于直线
相交于点A,B,是否存在这样的实数a,使得A,B关于直线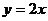 对称?如果存在,求出实数a,如果不存在,请说明理由。
对称?如果存在,求出实数a,如果不存在,请说明理由。
 答案:设存在实数a,使得A,B关于y=2x对称,又设
答案:设存在实数a,使得A,B关于y=2x对称,又设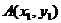 ,
,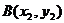 ,则
,则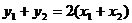 而
而 由
由 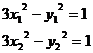 作差整理可得:
作差整理可得:
 由
由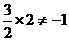 ,故不存在这样的实数a。
,故不存在这样的实数a。
错解: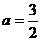
错因:没有挖掘隐含条件,而轴对称的第二个条件直线AB与直线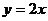 垂直,造成解题错误。
垂直,造成解题错误。
22.(薛中)设椭圆方程为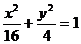 ,试求满足下列条件的圆方程:1圆心在椭圆的长轴上;2与椭圆的短轴相切;3与椭圆在某点处也相切。
,试求满足下列条件的圆方程:1圆心在椭圆的长轴上;2与椭圆的短轴相切;3与椭圆在某点处也相切。
答案:根据题意设圆方程为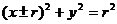 1,化椭圆方程为
1,化椭圆方程为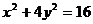 2,由12消去y,得:
2,由12消去y,得: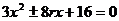 ,由圆与椭圆相切:
,由圆与椭圆相切: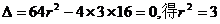 即所求圆的方程为:
即所求圆的方程为: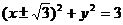 ,另由图可知
,另由图可知 也合题意。
也合题意。
错解: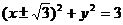
错因:漏解
21.(丁中)求经过点 且与双曲线
且与双曲线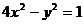 仅有一个公共点的直线方程。
仅有一个公共点的直线方程。
错解:无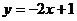 ,
,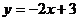 。
。
错因:把相切作为直线与双曲线有且仅有一个公共点的充要条件。
正 解:当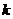 存在时,设所求直线方程为
存在时,设所求直线方程为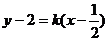 ,代入双曲线
,代入双曲线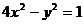 ,
,
得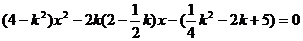
(1) 当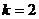 时,直线方程为
时,直线方程为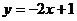 与双曲线只有一个公共点。
与双曲线只有一个公共点。
(2) 当 时,直线方程为
时,直线方程为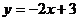 与双曲线只有一个公共点。
与双曲线只有一个公共点。
(3) 当直线和双曲线相切时,仅有一个公共点,此时有
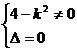 得
得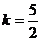 ,可得直线方程为
,可得直线方程为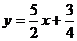
当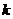 不存在时,直线
不存在时,直线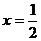 也满足题意。
也满足题意。
故经过点 且与双曲线
且与双曲线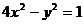 仅有一个公共点的直线方程有四条,它们分别为:
仅有一个公共点的直线方程有四条,它们分别为: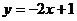 ,
,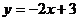 ,
,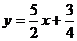 ,
,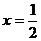 。
。
20.(丁中)已知双曲线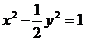 ,过点B(1,1)能否作直线
,过点B(1,1)能否作直线 ,使直线与双曲线交于
,使直线与双曲线交于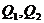 两点,且B是线段
两点,且B是线段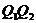 的中点?样的直线若存在,求出它的方程;若不存在,说明理由。
的中点?样的直线若存在,求出它的方程;若不存在,说明理由。
错解:直线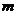 为
为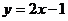 。
。
错因:忽视了直线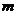 与双曲线交于
与双曲线交于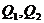 两点的隐含条件
两点的隐含条件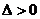 。
。
正解:假设存在直线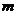 ,设
,设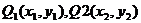 ,则有
,则有
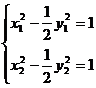
得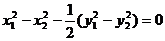
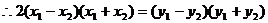
显然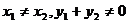
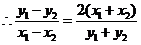
由中点公式得,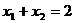 ,
,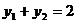
由斜率公式得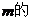 斜率
斜率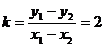
又使直线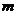 与双曲线交于
与双曲线交于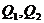 两点,由
两点,由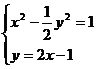 得
得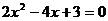 ,此方程必有两个不相等的实数根。而此时
,此方程必有两个不相等的实数根。而此时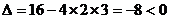 ,方程无实数根,即直线
,方程无实数根,即直线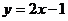 与双曲线
与双曲线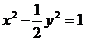 无交点,因此直线
无交点,因此直线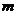 不存在。
不存在。
19.(丁中)直线y=kx+1与双曲线3x2-y2=1相交于不同的两点A、B:
(1)求实数k的取值范围;
(2)若以AB为直径的圆过坐标原点,求该圆的直径.
错解: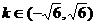
错因:由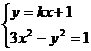 可得
可得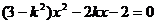 ,忽视
,忽视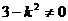 ,仅考虑
,仅考虑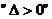
正解:k的取值范围是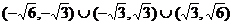
17.(丁中)已知点A(-2,-1)和B(2,3),圆C:x2+y2 = m2,当圆C与线段AB没有公共点时,求m的取值范围。
错解: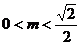 ,
,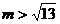
错因:将题中的实数m当成了圆的半径,误认为m>0。
正解: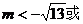
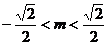
 且
且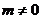
16.(一中)已知点N(1,2),过点N的直线交双曲线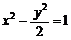 于A、B两点,且
于A、B两点,且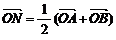
(1)求直线AB的方程;
(2)若过N的直线l交双曲线于C、D两点,且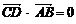 ,那么A、B、C、D四点是否共圆?为什么?
,那么A、B、C、D四点是否共圆?为什么?
解:(1)设直线AB: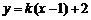 代入
代入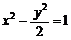 得
得
 (*)
(*)
令A(x1,y1),B(x2,y2),则x1、x2是方程的两根
∴ 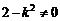 且
且 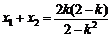
∵ 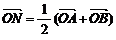 ∴ N是AB的中点
∴
∴ N是AB的中点
∴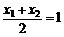
∴ 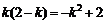 k = 1 ∴AB方程为:y
= x + 1
k = 1 ∴AB方程为:y
= x + 1
(2)将k = 1代入方程(*)得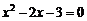
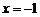 或
或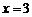
由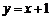 得
得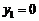 ,
,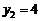
∴ 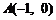 ,
,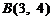
∵ 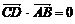 ∴ CD垂直平分AB ∴ CD所在直线方程为
∴ CD垂直平分AB ∴ CD所在直线方程为
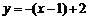 即
即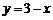 代入双曲线方程整理得
代入双曲线方程整理得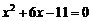
令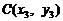 ,
,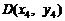 及CD中点
及CD中点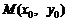
则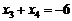 ,
,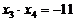 , ∴
, ∴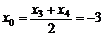 ,
, 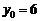
|CD| =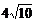 ,
,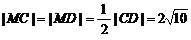
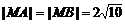 ,即A、B、C、D到M距离相等
,即A、B、C、D到M距离相等
∴ A、B、C、D四点共圆
15.(一中)如图所示,已知A、B、C是长轴长为4的椭圆上的三点,点A是长轴的一个端点,BC过椭圆中心O,且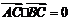 ,|BC|=2|AC|.
,|BC|=2|AC|.
 (I)建立适当的坐标系,求椭圆方程;
(I)建立适当的坐标系,求椭圆方程;
(II)如果椭圆上有两点P、Q,使∠PCQ的平分线垂直于AO,证明:存在实数λ,使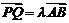 .
.
解:(I)以O为原点,OA为X轴建立直角坐标系,设A(2,0),则椭圆方程为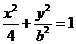
∵O为椭圆中心,∴由对称性知|OC|=|OB|
又∵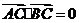 , ∴AC⊥BC
, ∴AC⊥BC
又∵|BC|=2|AC| ∴|OC|=|AC|
∴△AOC为等腰直角三角形
∴点C的坐标为(1,1) ∴点B的坐标为(-1,-1)
将C的坐标(1,1)代入椭圆方程得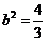 ,
,
则求得椭圆方程为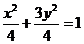
(II)由于∠PCQ的平分线垂直于OA(即垂直于x轴),不妨设PC的斜率为k,则QC的斜率为-k,因此PC、QC的直线方程分别为y=k(x-1)+1,y=-k(x-1)+1
由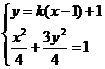 得(1+3k2)x2-6k(k-1)x+3k2-6k-1=0 *)
得(1+3k2)x2-6k(k-1)x+3k2-6k-1=0 *)
∵点C(1,1)在椭圆上,
∴x=1是方程(*)的一个根,∴xP•1= 即xP=
即xP=
同理xQ=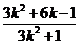
∴直线PQ的斜率为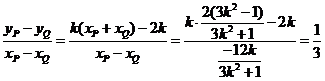 (定值)
(定值)
又∠ACB的平分线也垂直于OA
∴直线PQ与AB的斜率相等(∵kAB=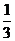 )
)
∴向量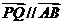 ,即总存在实数
,即总存在实数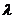 ,使
,使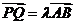 成立.
成立.

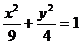 有公共顶点,且离心率为
有公共顶点,且离心率为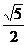 的双曲线方程.
的双曲线方程.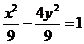
 ,
,