16.(一中)已知点N(1,2),过点N的直线交双曲线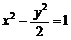 于A、B两点,且
于A、B两点,且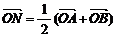
(1)求直线AB的方程;
(2)若过N的直线l交双曲线于C、D两点,且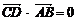 ,那么A、B、C、D四点是否共圆?为什么?
,那么A、B、C、D四点是否共圆?为什么?
解:(1)设直线AB: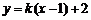 代入
代入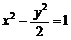 得
得
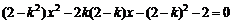 (*)
(*)
令A(x1,y1),B(x2,y2),则x1、x2是方程的两根
∴ 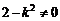 且
且 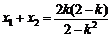
∵ 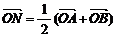 ∴ N是AB的中点
∴
∴ N是AB的中点
∴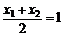
∴ 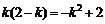 k = 1 ∴AB方程为:y
= x + 1
k = 1 ∴AB方程为:y
= x + 1
(2)将k = 1代入方程(*)得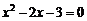
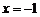 或
或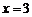
由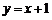 得
得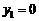 ,
,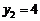
∴ 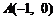 ,
,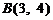
∵ 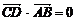 ∴ CD垂直平分AB ∴ CD所在直线方程为
∴ CD垂直平分AB ∴ CD所在直线方程为
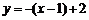 即
即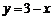 代入双曲线方程整理得
代入双曲线方程整理得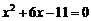
令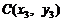 ,
,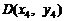 及CD中点
及CD中点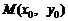
则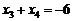 ,
,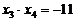 , ∴
, ∴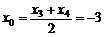 ,
, 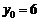
|CD| =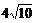 ,
,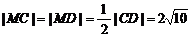
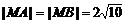 ,即A、B、C、D到M距离相等
,即A、B、C、D到M距离相等
∴ A、B、C、D四点共圆
- 答案

