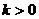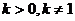29．(丁中)过双曲线x²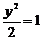－的右焦点作直线交双曲线于A、B两点，且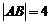，则这样的直线有___________条。

错解：2

错因：设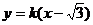代入椭圆的方程算出有两条，当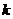不存在，即直线AB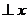轴时，

｜AB｜＝4，忽视此种情况。

正解：3

28．(丁中)如果方程x²+ky²=2表示椭圆，那么实数k的取值范围是____________

错解：

错因：忽视圆是椭圆的特殊情况。

正解：

27．(丁中)已知圆方程为x²+y²+8x+12=0,在此圆的所有切线中，纵横截距相等的条数有____________

错解：2

错因：忽视过原点的直线纵横截距相等

正解：4

26．(丁中)过圆外一点P(5，－2)作圆x²+y²－4x－4y=1的切线，则切线方程为__________。

错解：3x+4y－7 = 0

错因：忽视斜率不存在的情况，导致缺解。

正解：3x+4y－7 = 0或x = 5　

25．(丁中)已知、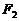是椭圆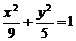的左、右焦点，P为椭圆上一个点，且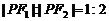，则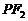的斜率为____________．

错解: 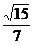或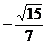

错因:忽视对称性,只求出一解.

正解: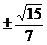

24．(丁中)已知直线x=a和圆(x－1)²+y²=4相切，那么实数a的值为_______________

错解：a = 3

错因：只考虑一种情况。

正解：a = 3或a =－1　

正解：5

23．(丁中)．已知直线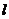与点A(3，3)和B(5，2)的距离相等，且过二直线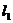：3x－y－1=0和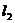：x+y－3=0的交点，则直线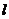的方程为　　　　　　　　　

错解：x+2y－5 = 0　

错因：应该有两种可能，忽视经过AB中点的情况。

正解：x－6y+11 = 0或x+2y－5 = 0　

22．(江安中学)一双曲线与椭圆有共同焦点，并且与其中一个交点的纵坐标为4，则这个双曲线的方程为_____。

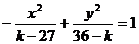正解：-，设双曲线的方程为 (27)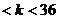

又由题意知 　

故所求双曲线方程为

误解：不注意焦点在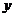轴上，出现错误。

21．(蒲中)若方程(9－m)x²+(m－4)y²=1表示椭圆，则实数m的取值范围是_________

答案：4<m<9且m

点评：易误填：4<m<9，而忽略方程可能表示圆的情况。

20．(蒲中)已知a、b、c分别是双曲线的实半轴、虚半轴和半焦距，若方程ax²+bx+c=0无实根，则此双曲线的离心率e的取值范围是___________

答案：1<e<2+

点评：易忽视双曲线离心率的基本范围“e>1”。