6.在正四面体P-ABC中,D,E,F分别是AB,BC,CA的中点,下面四个结论中不成立的是 ( )
A.BC//平面PDF B.DF⊥PAE
C.平面PDF⊥平面ABC D.平面PAE⊥平面ABC
[答案]C
[详解]
如图所示:DF∥BC可得A正确
 可得
可得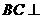 平面
平面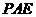
从而得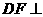 平面
平面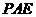 B正确
B正确
 平面ABC 则平面
平面ABC 则平面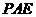
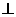 平面ABC D正确
平面ABC D正确
[名师指津]
立体几何中的几个重要模型正四面体、正三棱锥、正四棱等中的边边、边面、面面
之间的关系为这一章节的重点内容,高考题的大部分题目都以它们为背景.
5.对任意的锐角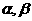 ,下列不等关系中正确的是 ( )
,下列不等关系中正确的是 ( )
A.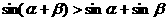 B.
B.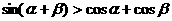
C.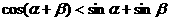 D.
D.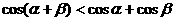
[答案]D
[详解]
当 时可排除A、B选项,当
时可排除A、B选项,当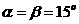 时代入C选项中,即:
时代入C选项中,即: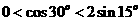
两边平方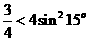
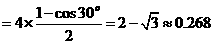 矛盾故选D
矛盾故选D
[名师指津]
特殊值反代入的解题思想在高考选择题的解决过程中经常用到.本题只是简单的两组特殊角代
入即可解决问题.特殊值解选择题关键是恰到好处地选取特殊值如:数值类经常考虑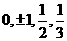
角类的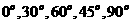 真数类
真数类 ,底的
,底的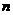 次幂或是
次幂或是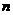 次幂的倒数等等
次幂的倒数等等
4.从原点向圆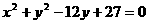 作两条切线,则该圆夹在两条切线间的劣弧长为( )
作两条切线,则该圆夹在两条切线间的劣弧长为( )
A.π B.2π C.4π D.6π
[答案]B
[详解]
将圆的方程配方得: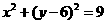 圆心在
圆心在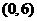 半径为3,如图:
半径为3,如图:
在图中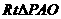 中,
中,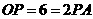 ,从而得到
,从而得到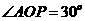 ,
,
即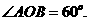 可求
可求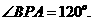
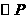 的周长为
的周长为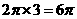
劣弧长为周长的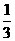 ,可求得劣弧长为
,可求得劣弧长为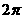 .
.
[名师指津]
以数形结合的思想解决此类题,抓图中直角三角形中边角关系.
3.| a |=1,| b |=2,c = a + b,且c⊥a,则向量a与b的夹角为 ( )
A.30° B.60° C.120° D.150°
[答案]C
[详解]
设所求两向量的夹角为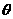
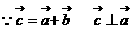
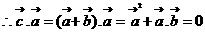
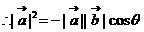 即:
即: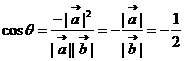
所以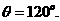
[名师指津]
对于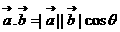 这个公式的变形应用应该做到熟练,另外向量垂直(平行)的充要条件
这个公式的变形应用应该做到熟练,另外向量垂直(平行)的充要条件
 必需掌握.
必需掌握.
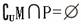
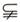
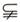 1.设合集U=R,集合
1.设合集U=R,集合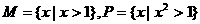 ,则下列关系中正确的是( )
,则下列关系中正确的是( )
A.M=P B.P M C.M P D.
[答案]C
[详解]
 或
或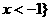

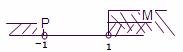
易得M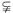 P
P
[名师指津]
集合与集合之间关系的题目经常助图象来观察.
2.“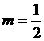 ”是“直线
”是“直线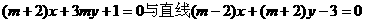 相互垂直”的 ( )
相互垂直”的 ( )
A.充分必要条件 B.充分而不必要条件
C.必要而不充分条件 D.既不充分也不必要条件
[答案]B
[详解]
当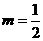 时两直线斜率乘积为
时两直线斜率乘积为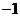 从而可得两直线垂直,当
从而可得两直线垂直,当 时两直线一条斜率为0一条
时两直线一条斜率为0一条
斜率不存在,但两直线仍然垂直.因此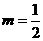 是题目中给出的两条直线垂直的充分但不必要条
是题目中给出的两条直线垂直的充分但不必要条
件.
[名师指津]
对于两条直线垂直的充要条件①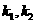 都存在时
都存在时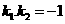 ②
②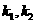 中有一个不存在另一个为零
中有一个不存在另一个为零
对于②这种情况多数考生容易忽略.
21.(本小题满分12分)
设直线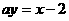 与抛物线
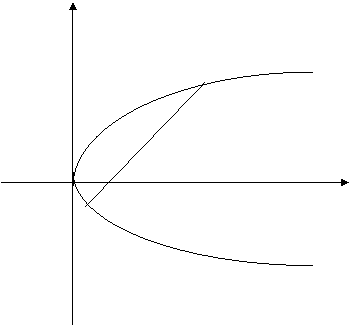
与抛物线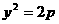 交于相异两点A、B,以线段AB为直经作圆H(H为圆心). 试证抛物线顶点在圆H的圆周上;并求a的值,使圆H的面积最小.
交于相异两点A、B,以线段AB为直经作圆H(H为圆心). 试证抛物线顶点在圆H的圆周上;并求a的值,使圆H的面积最小.
|
|
|

|
|
|
|
|
20.(本小题满分12分)
某工厂生产某种产品,已知该产品的月生产量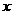 (吨)与每吨产品的价格
(吨)与每吨产品的价格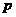 (元/吨)之间的关系式为:
(元/吨)之间的关系式为: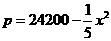 ,且生产x吨的成本为
,且生产x吨的成本为 (元).问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(利润=收入─成本)
(元).问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(利润=收入─成本)
19.(本小题满分12分)
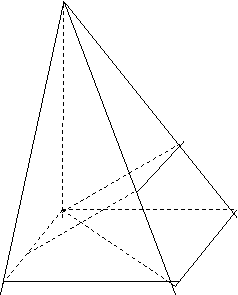
如图,四棱锥P-ABCD的底面是正方形, 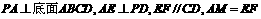
(1) 证明MF是异面直线AB与PC的公垂线;
(2)若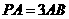 ,求二面角E-AB-D平面角.
,求二面角E-AB-D平面角.
|
|
|
|
|
|
|
|
18.(本小题满分12分)
设甲、已、丙三人每次射击命中目标的概率分别为0.7、0.6和0.5。
(1)三人各向目标射击一次,求至少有一人命中目标的概率及恰有两人命中目标的概率;
(2)若甲单独向目标射击三次,求他恰好命中两次的概率.

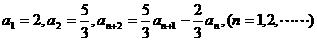
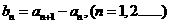 求数列
求数列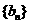 的通项公式;
的通项公式; 的前n项和
的前n项和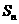 .
.