16.(本小题共14分)
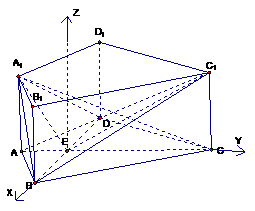
 如图,在直四棱柱ABCD-A1B1C1D1中,AB=AD=2,DC=
如图,在直四棱柱ABCD-A1B1C1D1中,AB=AD=2,DC= ,
,
AC⊥BD,垂足为E.
(Ⅰ)求证BD⊥A1C;
(Ⅱ)求二面角A1-BD-C1的大小;
(Ⅲ)求异面直线AD与BC1所成角的余弦值.
 解法一:
解法一:
(I)在直四棱柱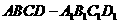 中,
中,
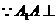 底面
底面 ,
,
 是
是 在平面
在平面 上的射影.
上的射影.

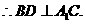
(II)连结
与(I)同理可证
 为二面角
为二面角 的平面角.
的平面角.
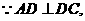
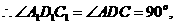
又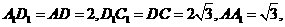 且
且

在 中,
中, ,
,  ,
,
即二面角 的大小为90°
的大小为90°
(III)过B作BF∥AD交 于
于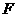 ,连结
,连结
则 就是
就是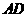 与
与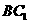 所成的角.
所成的角.


在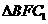 中,
中, 。
。
即异面直线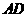 与
与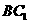 所成角的余弦值为
所成角的余弦值为 。
。
 解法二:
解法二:
(I)同解法一.
(II)如图,以D为坐标原点,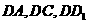 所
所
在直线分别为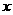 轴,
轴, 轴,
轴, 轴,建立空间
轴,建立空间
直角坐标系.
连结
与(I)同理可证,
 为二面角
为二面角 的平面角.
的平面角.

得 。
。
∴ 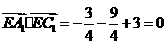 。∴
。∴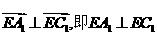 。
。
∴ 二面角 的大小为90°.
的大小为90°.
(II)如图,由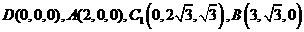 ,得
,得 。
。
∵  ,
,
∴ 。
。
即异面直线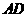 与
与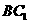 所成角的余弦值为
所成角的余弦值为 。
。
解法三:
(I)同解法一.
 (II)如图,建立空间直角坐标,坐标原点为E.
(II)如图,建立空间直角坐标,坐标原点为E.
连结
与(I)同理可证,
 为二面角
为二面角 的平面角.
的平面角.
由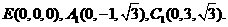
得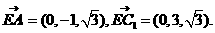

 二面角
二面角 的大小为
的大小为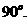
(III)如图,由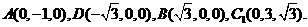
得

 异面直线
异面直线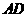 与
与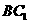 所成角的大小为
所成角的大小为
[名师指津]
三垂线定理,二面角的平面角、线面角、两条异面直线所成的角作法及求法,线线、线面、面面平
行与直线的判断与性质,构成了立体几何的主要内容,平时学习时应将之落实.
15.(本小题共13分)
已知函数
(Ⅰ)求 的单调减区间;
的单调减区间;
(Ⅱ)若 在区间[-2,2].上的最大值为20,求它在该区间上的最小值.
在区间[-2,2].上的最大值为20,求它在该区间上的最小值.
[答案]
[详解]
解:(I)
令 ,解得
,解得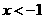 或
或
所以函数 的单调递减区间为
的单调递减区间为
(II)因为

所以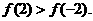
因为在 上
上 ,所以
,所以 在
在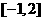 单调递增,又由于
单调递增,又由于
 在
在 上单调递减,因此
上单调递减,因此 和
和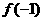 分别是
分别是 在区间
在区间
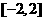 上的最大值和最小值.
上的最大值和最小值.
于是有 ,解得
,解得
故
因此
即函数 在区间
在区间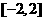 上的最小值为
上的最小值为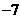

[名师指津]
函数求导的方法研究函数的单调性及最值问题近几年高考试题中屡屡出现,成为热门题型.要
熟练掌握各种常见函数的求导方法及研究单调、最值的基本思路.
14.已知n次式项式 .
.
如果在一种算法中,计算 的值需要k-1次乘法,计算P3(x0)的值共需要9次运算(6次乘法,3次加法),那么计算P10(x0)的值共需要
的值需要k-1次乘法,计算P3(x0)的值共需要9次运算(6次乘法,3次加法),那么计算P10(x0)的值共需要
次运算.
下面给出一种减少运算次数的算法:P0(x)=a0,Pk+1(x)=xPk(x)+ak+1(k=0,1,2,…,n-1).利用该算法,计算P3(x0)的值共需要6次运算,计算P10(x0)的值共需要
次运算.
[答案]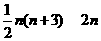
[详解]
由题意知道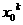 的值需要
的值需要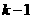 次运算,即进行
次运算,即进行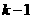 次
次 的乘法运算可得到
的乘法运算可得到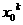 的结果
的结果
对于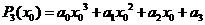 这里
这里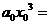
 进行了3次运算,
进行了3次运算,
 进行了2次运算,
进行了2次运算, 进行1次运算,最后
进行1次运算,最后 之间的加法
之间的加法
运算进行了3次这样 总共进行了
总共进行了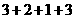
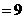 次运算
次运算
对于
 总共进行了
总共进行了 次
次
乘法运算及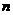 次加法运算所总共进行了
次加法运算所总共进行了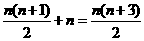 次
次
由改进算法可知:
 ,
,

 ,
,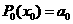
运算次数从后往前算和为: 次
次
[名师指津]
本题目属于信息题,做此类题需要认真分析题目本身所给的信息.
13.对于函数 定义域中任意的
定义域中任意的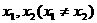 ,有如下结论:
,有如下结论:
①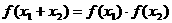 ; ②
; ②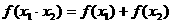 ;
;
③ ④
④
当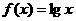 时,上述结论中正确结论的序号是
.
时,上述结论中正确结论的序号是
.
[答案]②③
[详解]
对于①②可以用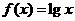
直接验证即可②满足题意
对于③④如右图所示:
对于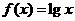 图象上任意不同
图象上任意不同
两点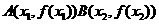
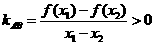 显然成立(可以用
显然成立(可以用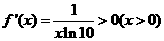 )故③正确
)故③正确
再有AB中点C(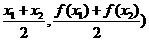 过C作
过C作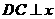 轴交
轴交 于D(
于D(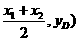
D在 上有:
上有: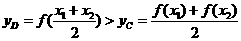 故④不正确
故④不正确
[名师指津]
本题主要考查了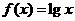 函数运算性质以及直线斜率应用,题目较综合.
函数运算性质以及直线斜率应用,题目较综合.
11.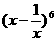 的展开式中的常数项是
. (用数字作答)
的展开式中的常数项是
. (用数字作答)
[答案]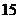
[详解]
对于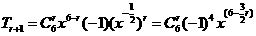 当
当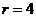 时第5项为常数项,即
时第5项为常数项,即
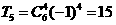 .
.
[名师指津]
二项式定理第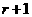 项的通项公式
项的通项公式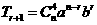 的运用在往年高考中经常遇到.
的运用在往年高考中经常遇到.
10.已知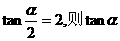 的值为
,
的值为
,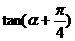 的值为
.
的值为
.
[答案]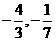
[详解]
(I)因为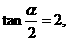
所以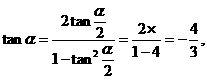
所以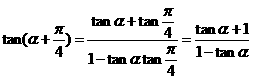
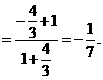
[名师指津]
本题还考查了倍角的正切公式与两角和的正公式.三角函数知识的考查每年题目难度都不是很
大,应该抓基本公式与基本题型的解决.
9.若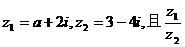 为纯虚数,则实数a的值为
.
为纯虚数,则实数a的值为
.
[答案]
[详解]

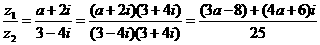 为纯虚数
为纯虚数
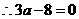 且
且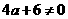
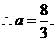
[名师指津]
复数的四则运算,复数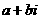 为实数、纯虚数的充要条件,复数的模作为复数内容的重点.
为实数、纯虚数的充要条件,复数的模作为复数内容的重点.
8.函数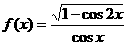 ( )
( )
A.在 上递减
上递减
B.在 上递减
上递减
C.在 上递减
上递减
D.在 上递减
上递减
[答案]A
[详解]
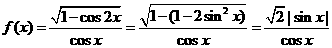
当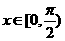 或
或 时
时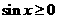
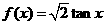 在
在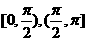 上为增函数
上为增函数
当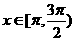 或
或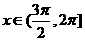 时
时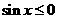
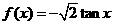 在
在 上为减函
上为减函
数.
[名师指津]
对二倍角余弦公式及两个变式的的正用逆用应熟练,对处理绝对值问题的基本思路是用分类
讨论的思想去掉绝对值然后再研究问题,正切函数的单调区间.
第Ⅱ卷(共110分)
7.北京《财富》全球论坛期间,某高校有14名志愿者参加接待工作,若每天早、中、晚三班,每4人,每人每天最多值一班,则开幕式当天不同的排班种数为 ( )
A. B.
B.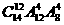 C.
C. D.
D.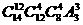
[答案]A
[详解]
本题可以先从14人中选出12人即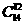 ,然后从这12人中再选出4人做为早班即
,然后从这12人中再选出4人做为早班即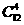 ,最后再从剩
,最后再从剩
余的8人选出4人安排为中班即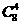 ,剩下的4个安排为晚班,以上为分步事件应用乘法原理可得
,剩下的4个安排为晚班,以上为分步事件应用乘法原理可得
不同的排法为: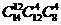 .
.
[名师指津]
排列组合中的分步计数原理与分类计数原理做为解决此类问题的基础.

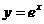 的切线,则切点的坐标为
,切线的斜率为 .
的切线,则切点的坐标为
,切线的斜率为 .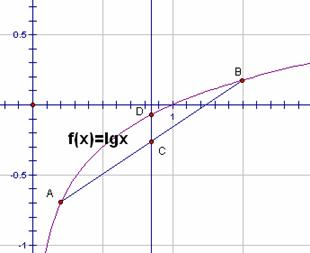 [答案]
[答案]
