(17)(本小题满分12分)

在,求

(1)

(2)若点

(18)(本小题满分12分)

设等比数列的前n项和为，

(19)(本小题满分12分)

某批产品成箱包装，每箱5件，一用户在购进该批产品前先取出3箱，再从每箱中任意出取2件产品进行检验。设取出的第一、二、三箱中分别有0件、1件、2件二等品，其余为一等品。

(I)求取6件产品中有1件产品是二等品的概率。

(II)若抽检的6件产品中有2件或2件以上二等品，用户就拒绝购买这批产品，求这批产品被用户拒绝的概率。

(20)(本小题12分)

如图，在直三棱柱中，、分别为、的中点。

(I)证明：ED为异面直线与的公垂线；

(II)设求二面角的大小

(21)(本小题满分为14分)

设，函数若的解集为A，，求实数的取值范围。

(22)(本小题满分12分)

已知抛物线的焦点为F，A、B是抛物线上的两动点，且过A、B两点分别作抛物线的切线，设其交点为M。

(I)证明为定值；

(II)设的面积为S，写出的表达式，并求S的最小值。

普通高等学校招生全国统一考试(全国II卷)

(13)在的展开式中常数项是＿＿＿＿＿。(用数字作答)

(14)圆是以为半径的球的小圆，若圆的面积和球的表面积的比为，则圆心到球心的距离与球半径的比＿＿＿＿＿。

(15)过点的直线将圆分成两段弧，当劣弧所对的圆心角最小时，直线的斜率

(16)一个社会调查机构就某地居民的月收入调查了10000人，并根据所得数据画了样本的频率分布直方图(如下图)。为了分析居民的收入与年龄、学历、职业等方面的关系，要从这10000人中再用分层抽样方法抽出100人作进一步调查，则在(元)月收入段应抽出＿＿＿＿＿人。

(1)已知向量＝(4，2)，向量＝(，3)，且//,则＝(　 )

(A)9　　 (B)6　　 (C)5　　 (D)3

(2)已知集合，则(　 )

(A)　　 (B)　　 (C)　　 (D)

(3)函数的最小正周期是(　 )

(A)　　(B)　　(C)　　(D)

(4)如果函数的图像与函数的图像关于坐标原点对称，则的表达式为(　 )

(A)　(B)　 (C)　(D)

(5)已知的顶点B、C在椭圆上，顶点A是椭圆的一个焦点，且椭圆的另外一个焦点在BC边上，则的周长是(　 )

(A)　　(B)6　　(C)　　(D)12

(6)已知等差数列中，，则前10项的和＝(　 )

(A)100　　 (B)210　　 (C)380　　 (D)400

(7)如图，平面平面，与两平面、所成的角分别为和。过A、B分别作两平面交线的垂线，垂足为、若AB=12,则(　 )

(A)4　　(B)6　　 (C)8　　(D)9

(8)已知函数，则的反函数为(　 )

(A)　　(B)

(C)　　(D)

(9)已知双曲线的一条渐近线方程为，则双曲线的离心率为(　 )

(A)　　(B)　　(C)　　(D)

(10)若则(　 )

(A)　(B)　 (C)　(D)

(11)过点(－1，0)作抛物线的切线，则其中一条切线为(　 )

(A) (B) (C) (D)

(12)5名志愿者分到3所学校支教，每个学校至少去一名志愿者，则不同的分派方法共有(　 )

(A)150种　　 (B)180种　　 (C)200种　　 (D)280种

第Ⅱ卷

(17)(本小题满分12分)

已知向量a＝(sinθ，1)，b＝(1，cosθ)，－＜θ＜．

(Ⅰ)若a⊥b，求θ；

(Ⅱ)求｜a+b｜的最大值．

(18)(本小题满分12分)

某批产品成箱包装，每箱5件．一用户在购进该批产品前先取出3箱，再从每箱中任意抽取2件产品进行检验．设取出的第一、二、三箱中分别有0件、1件、2件二等品，其余为一等品．

(Ⅰ)用ξ表示抽检的6件产品中二等品的件数，求ξ的分布列及ξ的数学期望；

(Ⅱ)若抽检的6件产品中有2件或2件以上二等品，用户就拒绝购买这批产品，求这批产品级用户拒绝的概率．

(19)(本小题满分12分)

如图，在直三棱柱ABC－A₁B₁C₁中，AB＝BC，D、E分别为BB₁、AC₁的中点．

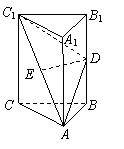(Ⅰ)证明：ED为异面直线BB₁与AC₁的公垂线；

(Ⅱ)设AA₁＝AC＝AB，求二面角A₁－AD－C₁的大小．

(20)(本小题满分12分)

设函数f(x)＝(x+1)ln(x+1)，若对所有的x≥0，都有f(x)≥ax成立，求实数a的取值范围．

(21)(本小题满分14分)

已知抛物线x²＝4y的焦点为F，A、B是抛物线上的两动点，且＝λ(λ＞0)．过A、B两点分别作抛物线的切线，设其交点为M．

(Ⅰ)证明·为定值；

(Ⅱ)设△ABM的面积为S，写出S＝f(λ)的表达式，并求S的最小值．

(22)(本小题满分12分)

设数列{a_n}的前n项和为S_n，且方程x²－a_nx－a_n＝0有一根为S_n－1，n＝1，2，3，…．

(Ⅰ)求a₁，a₂；

(Ⅱ){a_n}的通项公式．

普通高等学校招生全国统一考试

(13)在(x⁴+)¹⁰的展开式中常数项是　　　　　　　 (用数字作答)

(14)已知△ABC的三个内角A、B、C成等差数列，且AB＝1，BC＝4，则边BC上的中线AD的长为　　　　　　　　 ．

(15)过点(1，)的直线l将圆(x－2)²+y²＝4分成两段弧，当劣弧所对的圆心角最小时，直线l的斜率k＝　　　　　　 ．

(16)一个社会调查机构就某地居民的月收入调查了10 000人，并根据所得数据画了样本的频率分布直方图(如下图)．为了分析居民的收入与年龄、学历、职业等方面的关系，要从这10 000人中再用分层抽样方法抽出100人作进一步调查，则在［2500，3000)(元)月收入段应抽出　　　　　　　 人．

(1)已知集合M＝{x|x＜3}，N＝{x|log₂x＞1}，则M∩N＝

(A)　　　　　　　　　　　　 (B){x|0＜x＜3}

(C){x|1＜x＜3}　　　　　　　　 (D){x|2＜x＜3}

(2)函数y＝sin2xcos2x的最小正周期是

(A)2π　　　　　 (B)4π　　　　 (C)　　　　　 (D)

(3)＝

(A)i　　　　　 (B)－i　　　　 (C)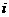　　　　　 (D)－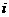

(4)过球的一条半径的中点，作垂直于该半径的平面，则所得截面的面积与球的表面积的比为

(A)　　　　　　 (B)　　　　　　 (C)　　　　　　　 (D)

(5)已知△ABC的顶点B、C在椭圆+y²＝1上，顶点A是椭圆的一个焦点，且椭圆的另外一个焦点在BC边上，则△ABC的周长是

(A)2　　　　　　 (B)6　　　　　 (C)4　　　　 (D)12

(6)函数y＝lnx－1(x＞0)的反函数为

(A)y＝e^x+1(x∈R)　　　　　　　　　　　 (B)y＝e^x－1(x∈R)

(C)y＝e^x+1(x＞1)　　　　　　　　　　　　 (D)y＝e^x－1(x＞1)

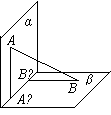(7)如图，平面α⊥平面β，A∈α，B∈β，AB与两平面α、β所成的角分别为和，过A、B分别作两平面交线的垂线，垂足为A′、B′，则AB∶A′B′＝

(A)2∶1　　　　　　　 (B)3∶1

(C)3∶2　　　　　　　 (D)4∶3

(8)函数y＝f(x)的图像与函数g(x)＝log₂x(x＞0)的图像关于原点

对称，则f(x)的表达式为

(A)f(x)＝(x＞0)　　　　　 (B)f(x)＝log₂(－x)(x＜0)

(C)f(x)＝－log₂x(x＞0)　　　　 (D)f(x)＝－log₂(－x)(x＜0)

(9)已知双曲线的一条渐近线方程为y＝x，则双曲线的离心率为

(A)　　　　　　 (B)　　　　　 (C)　　　　　　 (D)

(10)若f(sinx)＝3－cos2x，则f(cosx)＝

(A)3－cos2x　　　　 (B)3－sin2x　　　　 (C)3+cos2x　　　 (D)3+sin2x

(11)设S_n是等差数列{a_n}的前n项和，若＝，则＝

(A)　　　　　 (B)　　　　　　　　　 (C)　　　　　 (D)

(12)函数f(x)＝的最小值为

(A)190　　　　　 (B)171　　　　　　 (C)90　　　　 (D)45

绝密★启用前

普通高等学校招生全国统一考试数学103

第Ⅱ卷

(本卷共10小题，共90分)

22. 解: f ' (x)=3x²－2ax+(a²－1),其判别式△=4a²－12a²+12=12－8a².

(ⅰ)若△=12－8a²=0,即 a=±, 当x∈(－∞,), 或x∈( , +∞)时, f '(x)>0, f(x)在(－∞,+ ∞)为增函数. 所以a=±.

　(ⅱ)若△=12－8a²<0, 恒有f '(x)>0, f(x)在(－∞,+ ∞)为增函数, 所以a²> ,

即 a∈(－∞,－ )∪( , +∞)

(ⅲ)若△12－8a²>0,即－ <a<, 令f '(x)=0, 解得 x₁=, x₂=.

当x∈(－∞,x₁),或x∈(x₂,+ ∞)时, f '(x)>0, f(x)为增函数; 当x∈(x₁,x₂)时 , f '(x)<0,f(x)为减函数. 依题意x₁≥0且x₂≤1. 由x₁≥0得a≥,解得 1≤a<

由x₂≤1得≤3－a, 解得 － <a< , 从而 a∈[1, )

综上,a的取值范围为(－∞,－ ]∪[ , +∞) ∪[1, ),即a∈(－∞,－ ]∪[1,∞).

21. 解: 依题意可设P(0,1),Q(x,y),则 |PQ|=,又因为Q在椭圆上,

所以,x²=a²(1－y²) , |PQ|²= a²(1－y²)+y²－2y+1=(1－a²)y²－2y+1+a²

　　　 =(1－a²)(y－ )²－+1+a² .

因为|y|≤1,a>1, 若a≥, 则||≤1, 当y=时, |PQ|取最大值;

若1<a<,则当y=－1时, |PQ|取最大值2.

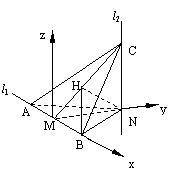
20.解法一: (Ⅰ)由已知l₂⊥MN, l₂⊥l₁ , MN∩l₁ =M, 可得l₂⊥平面ABN.由已知MN⊥l₁ , AM=MB=MN,可知AN=NB且AN⊥NB. 又AN为AC在平面ABN内的射影.

∴AC⊥NB

(Ⅱ)∵Rt△CAN≌Rt△CNB, ∴AC=BC,又已知∠ACB=60°,因此△ABC为正三角形.

∵Rt△ANB≌Rt△CNB, ∴NC=NA=NB,因此N在平面ABC内的射影H是正三角形ABC的中心,连结BH,∠NBH为NB与平面ABC所成的角.

在Rt△NHB中,cos∠NBH= = = .

解法二: 如图,建立空间直角坐标系M－xyz.令MN=1, 则有A(－1,0,0),B(1,0,0),N(0,1,0),

(Ⅰ)∵MN是 l₁、l₂的公垂线, l₁⊥l₂, ∴l₂⊥平面ABN. l₂平行于z轴. 故可设C(0,1,m).于是 =(1,1,m), =(1,－1,0). ∴·=1+(－1)+0=0　 ∴AC⊥NB.

(Ⅱ)∵ =(1,1,m), =(－1,1,m), ∴||=||, 又已知∠ACB=60°,∴△ABC为正三角形,AC=BC=AB=2. 在Rt△CNB中,NB=, 可得NC=,故C(0,1, ).

连结MC,作NH⊥MC于H,设H(0,λ, λ) (λ>0). ∴=(0,1－λ,－λ),

=(0,1, ). · = 1－λ－2λ=0, ∴λ= ,

∴H(0, , ), 可得=(0,, － ), 连结BH,则=(－1,, ),

∵·=0+ － =0, ∴⊥, 又MC∩BH=H,∴HN⊥平面ABC,

∠NBH为NB与平面ABC所成的角.又=(－1,1,0),

∴cos∠NBH= = 　=

19. 解: (1)设A_i表示事件“一个试验组中，服用A有效的小鼠有i只" , i=0,1,2,

B_i表示事件“一个试验组中，服用B有效的小鼠有i只" , i=0,1,2,

依题意有: P(A₁)=2×× = , P(A₂)= × = . P(B₀)= × = ,

P(B₁)=2× × = , 所求概率为: P=P(B₀·A₁)+P(B₀·A₂)+P(B₁·A₂)

= × + × + × =

(Ⅱ)所求概率为: P=1－(1－)³=