3.在△ABC中,∠C=90°, 则k的值是 ( )
则k的值是 ( )
A.5 B.-5 C.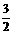 D.
D.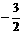
解:∵∠C=90°,∴ ,即((k-2,-2)·(2,3)=0,解得K=3,选(A)
,即((k-2,-2)·(2,3)=0,解得K=3,选(A)
(15)(本小题共12分)
已知 =2,求
=2,求
(I) 的值; (II)
的值; (II) 的值.
的值.
 (16)(本小题共14分)
(16)(本小题共14分)
如图, 在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点,
(I)求证:AC⊥BC1;
(II)求证:AC 1//平面CDB1;
(III)求异面直线 AC1与 B1C所成角的余弦值.
(17)数列{an}的前n项和为Sn,且a1=1,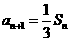 ,n=1,2,3,……,求
,n=1,2,3,……,求
(I)a2,a3,a4的值及数列{an}的通项公式;
(II) 的值.
的值.
(18)(本小题共13分)
甲、乙两人各进行3次射击,甲每次击中目标的概率为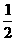 ,乙每次击中目标的概率
,乙每次击中目标的概率 ,
,
(I)甲恰好击中目标的2次的概率;
(II)乙至少击中目标2次的概率;
(III)求乙恰好比甲多击中目标2次的概率.
(19)(本小题共14分)
已知函数f(x)=-x3+3x2+9x+a,
(I)求f(x)的单调递减区间;
(II)若f(x)在区间[-2,2]上的最大值为20,求它在该区间上的最小值.

(20)(本小题共14分)
如图,直线 l1:y=kx(k>0)与直线l2:y=-kx之间的阴影区域(不含边界)记为W,其左半部分记为W1,右半部分记为W2.
(I)分别用不等式组表示W1和W2;
(II)若区域W中的动点P(x,y)到l1,l2的距离之积等于d2,求点P的轨迹C的方程;
(III)设不过原点O的直线l与(II)中的曲线C相交于M1,M2两点,且与l1,l2分别交于M3,M4两点.求证△OM1M2的重心与△OM3M4的重心重合.
(9)抛物线y2=4x的准线方程是 ;焦点坐标是 .
(10)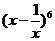 的展开式中的常数项是
(用数字作答)
的展开式中的常数项是
(用数字作答)
(11)函数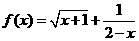 的定义域为
.
的定义域为
.
(12)在△ABC中,AC= ,∠A=45°,∠C=75°,则BC的长为
.
,∠A=45°,∠C=75°,则BC的长为
.
(13)对于函数f(x)定义域中任意的x1,x2(x1≠x2),有如下结论:
①f(x1+x2)=f(x1)·f(x2);② f(x1·x2)=f(x1)+f(x2); ③ >0;④
>0;④ .
.
当f(x)=lgx时,上述结论中正确结论的序号是 .
(14)已知n次多项式 ,
,
如果在一种算法中,计算 (k=2,3,4,…,n)的值需要k-1次乘法,计算
(k=2,3,4,…,n)的值需要k-1次乘法,计算 的值共需要9次运算(6次乘法,3次加法),那么计算
的值共需要9次运算(6次乘法,3次加法),那么计算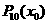 的值共需要
次运算.
的值共需要
次运算.
下面给出一种减少运算次数的算法: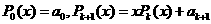 (k=0, 1,2,…,n-1).利用该算法,计算
(k=0, 1,2,…,n-1).利用该算法,计算 的值共需要6次运算,计算
的值共需要6次运算,计算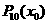 的值共需要
次运算.
的值共需要
次运算.
(1)设集合M={x| x>1,P={x| x2>1},则下列关系中正确的是
(A)M=P (B)P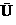 M (C)M
M (C)M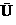 P ( D)
P ( D)
(2)为了得到函数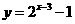 的图象,只需把函数
的图象,只需把函数 上所有点
上所有点
(A)向右平移3个单位长度,再向下平移1个单位长度
(B)向左平移3个单位长度,再向下平移1个单位长度
(C)向右平移3个单位长度,再向上平移1个单位长度
(D)向左平移3个单位长度,再向上平移1个单位长度
(3)“m=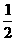 ”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直”的
”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直”的
(A)充分必要条件 (B)充分而不必要条件
(C)必要而不充分条件 (D)既不充分也不必要条件
(4)若 ,且
,且 ,则向量
,则向量 与
与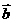 的夹角为
的夹角为
(A)30° (B)60° (C)120° (D)150°
(5)从原点向圆 x2+y2-12y+27=0作两条切线,则这两条切线的夹角的大小为
(A) (B)
(B)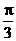 (C)
(C) (D)
(D)
(6)对任意的锐角α,β,下列不等关系中正确的是
(A)sin(α+β)>sinα+sinβ (B)sin(α+β)>cosα+cosβ
(C)cos(α+β)<sinα+sinβ (D)cos(α+β)<cosα+cosβ
(7)在正四面体P-ABC中,D,E,F分别是AB,BC,CA的中点,下面四个结论中不成立的是
(A)BC//平面PDF (B)DF⊥平面PA E
(C)平面PDF⊥平面ABC (D)平面PAE⊥平面 ABC
(8)五个工程队承建某项工程的五个不同的子项目,每个工程队承建1项,其中甲工程队不能承建1号子项目,则不同的承建方案共有
(A) 种 (B)
种 (B) 种 (C)
种 (C)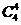 种 (D)
种 (D) 种
种
20.(本小题共14分)
设 是定义在[0,1]上的函数,若存在
是定义在[0,1]上的函数,若存在 上单调递增,在[x*,1]上单调递减,则称
上单调递增,在[x*,1]上单调递减,则称 为[0,1]上的单峰函数,x*为峰点,包含峰点的区间为含峰区间.
为[0,1]上的单峰函数,x*为峰点,包含峰点的区间为含峰区间.
对任意的[0,1]上的单峰函数 ,下面研究缩短其含峰区间长度的方法.
,下面研究缩短其含峰区间长度的方法.
(Ⅰ)证明:对任意的 为含峰区间;
为含峰区间;
若 为含峰区间;
为含峰区间;
(Ⅱ)对给定的r(0<r<0.5),证明:存在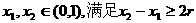 ,使得由(Ⅰ)所确定的含峰区间的长度不大于0.5+r;
,使得由(Ⅰ)所确定的含峰区间的长度不大于0.5+r;
(Ⅲ)选取 ,由(Ⅰ)可确定含峰区间为(0,
,由(Ⅰ)可确定含峰区间为(0, )或(
)或( ,1),在所得的含峰区间内选取
,1),在所得的含峰区间内选取 类似地可确定一个新的含峰区间,在第一次确定的含峰区间为(0,
类似地可确定一个新的含峰区间,在第一次确定的含峰区间为(0, )的情况下,试确定
)的情况下,试确定 的值,满足两两之差的绝地值不小于0.02,且使得新的含峰区间的长度缩短到0.34.
的值,满足两两之差的绝地值不小于0.02,且使得新的含峰区间的长度缩短到0.34.
(区间长度等于区间的右端点与左端点之差)
[答案]
[详解]
(I)证明:设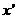 为
为 的峰点,则由单峰函数定义可知
的峰点,则由单峰函数定义可知 在
在 上单调递增,
上单调递增,
在 上单调递减.
上单调递减.
当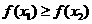 时,假设
时,假设 ,则
,则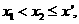 从而
从而
这与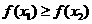 矛盾,所以
矛盾,所以 ,即
,即 是含峰区间.
是含峰区间.
当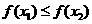 时,假设
时,假设 ,则
,则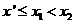 ,从而
,从而
这与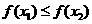 矛盾,所以
矛盾,所以 ,即
,即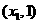 是含峰区间.
是含峰区间.
(II)证明:由(I)的结论可知:
当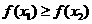 时,含峰区间的长度为
时,含峰区间的长度为
当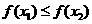 时,含峰区间的长度为
时,含峰区间的长度为
对于上述两种情况,由题意得
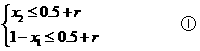
由①得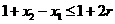 ,即
,即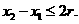
又因为 ,所以
,所以

将②代入①得

由①和③解得
所以这时含峰区间的长度 ,即存在
,即存在 使得所确定的含峰区间
使得所确定的含峰区间
的长度不大于
(III)解:对先选择的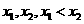 ,由(II)可知
,由(II)可知

在第一次确定的含峰区间为 的情况下,
的情况下,  的取值应满足
的取值应满足

由④与⑤可得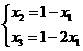
当 时,含峰区间的长度为
时,含峰区间的长度为
由条件 ,得
,得 ,从而
,从而
因此,为了将含峰区间的长度缩短到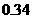 ,只要取
,只要取

[名师指津]
本题为信息题,通过题目中给出的信息结合已学过的数学知识解决这类问题.
19.(本小题共12分)
设数列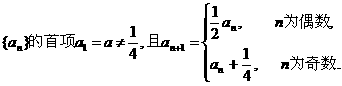
记
(Ⅰ)求a2,a3;
(Ⅱ)判断数列 是否为等比数列,并证明你的结论;
是否为等比数列,并证明你的结论;
(Ⅲ)求
[答案]
[详解]
解:(I)

(II)
因为 ,所以
,所以
所以
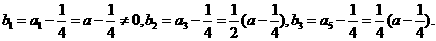
猜想: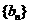 是公比为
是公比为 的等比数列.
的等比数列.
证明如下:
因为
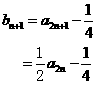

所以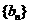 是首项为
是首项为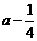 ,公比为
,公比为 的等比数列.
的等比数列.
(III)
[名师指津]
数列类型题,数列通项公式的递推公式经常在已知条件中给出,利用列举、叠加、叠乘等方法求之
通项公式的方法应掌握,另外递推公式与数学归纳法思想一致,数学归纳法证明方法经常在此类
题中运用.等差等比数列的通项公式及前 项和公式的求法和运用,等差等比数列的性质做为本
项和公式的求法和运用,等差等比数列的性质做为本
章复习的重点内容.
18.(本小题共14分)
如图,直线l1: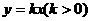 与直线l2:
与直线l2: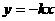 之间的阴影区域(不含边界)记为W,其左半部分记为W1,右半部分记为W2.
之间的阴影区域(不含边界)记为W,其左半部分记为W1,右半部分记为W2.
(Ⅰ)分别用不等式组表示W1和W2;
(Ⅱ)若区域W中的动点P(x,y)到l1,l2的距离之积等于d2,求点P的轨迹C的方程;
(Ⅲ)设不过原点O的直线l与(Ⅱ)中的曲线C相交于M1,M2两点,且与l1,l2分别
交于M3,M4两点. 求证△OM1M2的重心与△OM3M4的重心重合.

[答案]
[详解]
解:(I)
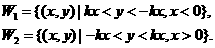
(II)直线 直线
直线 ,由题意得
,由题意得
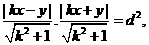
即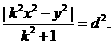
由 知
知
所以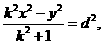 即
即
所以动点P的轨迹方程为
(III)当直线 与
与 轴垂直时,可设直线
轴垂直时,可设直线 的方程为
的方程为 由于直线
由于直线 、曲线C关于
、曲线C关于 轴对称,
轴对称,
且 与
与 关于
关于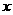 轴对称,于是
轴对称,于是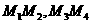 的中点坐标都为
的中点坐标都为 ,所以
,所以
的重心坐标都为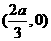 ,即它们的重心重合.
,即它们的重心重合.
当直线 与
与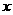 轴不垂直时,设直线
轴不垂直时,设直线 的方程为
的方程为
由 ,得
,得
由直线  与曲线C有两个不同交点,可知
与曲线C有两个不同交点,可知 ,且
,且

设 的坐标分别为
的坐标分别为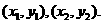
则
设 的坐标分别为
的坐标分别为
由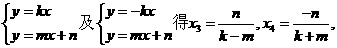
从而
所以
所以
于是 的重心与
的重心与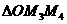 的重心也重合.
的重心也重合.
[名师指津]
本题为解析几何的综合题型,在高考试题中解析经常会与函数、数列、不等式、向量等综合考
查各种数学思想及方法.
17.(本小题共13分)
甲、乙两人各进行3次射击,甲每次击中目标的概率为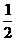 ,乙每次击中目标的概率为
,乙每次击中目标的概率为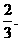
(Ⅰ)记甲击中目标的次数为ξ,求ξ的概率分布及数学期望Eξ;
(Ⅱ)求乙至多击中目标2次的概率;
(Ⅲ)求甲恰好比乙多击中目标2次的概率.
[答案]
[详解]
解:(I)

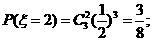
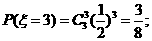
 的概率分布如下表:
的概率分布如下表:
 |
0 |
1 |
2 |
3 |
|
P |
 |
 |
 |
 |
 或
或
(II)乙至多击中目标2次的概率为
(III)设甲恰比乙多击中目标2次为事件A,甲恰击中目标2次且乙恰击中目标0次
为事件 ,甲恰击中目标3次且乙恰击中目标1次为事件
,甲恰击中目标3次且乙恰击中目标1次为事件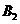 ,则
,则
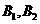 为互斥事件.
为互斥事件.

所以,甲恰好比乙多击中目标2次的概率为 .
.
[名师指津]
概率应用题在每年的各地高考试题中基本上都会有所涉及,而且本类题相对比较容易解决,复习时一定将这类题落实.

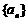 中,
中, ,则
,则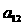 的值是 ( )
的值是 ( ) ,得a8=8,∴
,得a8=8,∴ ,∴a12=1+8×
,∴a12=1+8×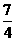 =15,选(A)
=15,选(A)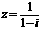 的共轭复数是 ( )
的共轭复数是 ( ) B.
B.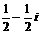 C.
C.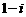 D.
D.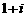
 选(B)
选(B)