17.解: 由A+B+C=π, 得 = - , 所以有cos =sin .
cosA+2cos =cosA+2sin =1-2sin2 + 2sin
=-2(sin - )2+
当sin = , 即A=时, cosA+2cos取得最大值为
⒄、(本小题满分12分)
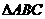 的三个内角为
的三个内角为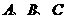 ,求当A为何值时,
,求当A为何值时,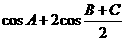 取得最大值,并求出这个最大值。
取得最大值,并求出这个最大值。
⒅、(本小题满分12分)
A、B是治疗同一种疾病的两种药,用若干试验组进行对比试验。每个试验组由4只小白鼠组成,其中2只服用A,另2只服用B,然后观察疗效。若在一个试验组中,服用A有效的小白鼠的只数比服用B有效的多,就称该试验组为甲类组。设每只小白鼠服用A有效的概率为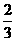 ,服用B有效的概率为
,服用B有效的概率为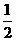 。
。
(Ⅰ)求一个试验组为甲类组的概率;
(Ⅱ)观察3个试验组,用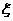 表示这3个试验组中甲类组的个数,求
表示这3个试验组中甲类组的个数,求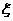 的分布列和数学期望。
的分布列和数学期望。
⒆、(本小题满分12分)
如图,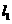 、
、 是互相垂直的异面直线,MN是它们的公垂线段。点A、B在
是互相垂直的异面直线,MN是它们的公垂线段。点A、B在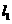 上,C在
上,C在 上,
上,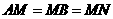 。
。
(Ⅰ)证明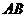 ⊥
⊥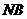 ;
;
(Ⅱ)若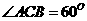 ,求
,求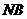 与平面ABC所成角的余弦值。
与平面ABC所成角的余弦值。
⒇、(本小题满分12分)
在平面直角坐标系 中,有一个以
中,有一个以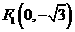 和
和 为焦点、离心率为
为焦点、离心率为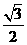 的椭圆,设椭圆在第一象限的部分为曲线C,动点P在C上,C在点P处的切线与
的椭圆,设椭圆在第一象限的部分为曲线C,动点P在C上,C在点P处的切线与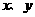 轴的交点分别为A、B,且向量
轴的交点分别为A、B,且向量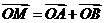 。求:
。求:
(Ⅰ)点M的轨迹方程;
(Ⅱ)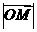 的最小值。
的最小值。
(21)、(本小题满分14分)
已知函数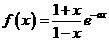 。
。
(Ⅰ)设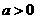 ,讨论
,讨论 的单调性;
的单调性;
(Ⅱ)若对任意 恒有
恒有 ,求
,求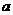 的取值范围。
的取值范围。
(22)、(本小题满分12分)
设数列 的前
的前 项的和
项的和
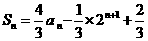 ,
,
(Ⅰ)求首项 与通项
与通项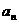 ;
;
(Ⅱ)设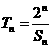 ,
, ,证明:
,证明: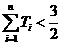
⒀、已知正四棱锥的体积为12,底面对角线的长为 ,则侧面与底面所成的二面角等于_______________。
,则侧面与底面所成的二面角等于_______________。
⒁、设 ,式中变量
,式中变量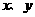 满足下列条件
满足下列条件

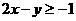
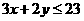

则z的最大值为_____________。
⒂、安排7位工作人员在5月1日到5月7日值班,每人值班一天,其中甲、乙二人都不能安排在5月1日和2日,不同的安排方法共有__________种。(用数字作答)
⒃、设函数 。若
。若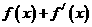 是奇函数,则
是奇函数,则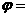 __________。
__________。
⑴、设集合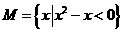 ,
,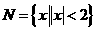 ,则
,则
A.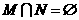 B.
B.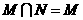
C.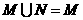 D.
D.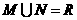
⑵、已知函数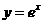 的图象与函数
的图象与函数 的图象关于直线
的图象关于直线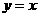 对称,则
对称,则
A.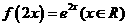 B.
B.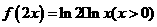
C.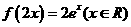 D.
D.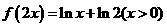
⑶、双曲线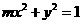 的虚轴长是实轴长的2倍,则
的虚轴长是实轴长的2倍,则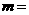
A.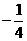 B.
B.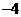 C.
C.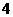 D.
D.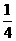
⑷、如果复数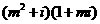 是实数,则实数
是实数,则实数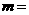
A.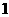 B.
B.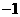 C.
C.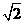 D.
D.
⑸、函数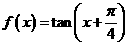 的单调增区间为
的单调增区间为
A.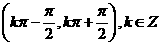 B.
B.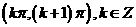
C.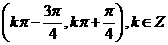 D.
D.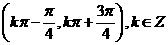
⑹、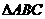 的内角A、B、C的对边分别为a、b、c,若a、b、c成等比数列,且
的内角A、B、C的对边分别为a、b、c,若a、b、c成等比数列,且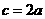 ,则
,则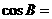
A.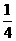 B.
B.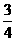 C.
C.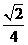 D.
D.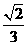
⑺、已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积是
A.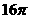 B.
B. C.
C.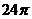 D.
D.
⑻、抛物线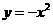 上的点到直线
上的点到直线 距离的最小值是
距离的最小值是
A.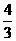 B.
B.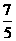 C.
C.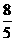 D.
D.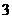
⑼、设平面向量 、
、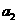 、
、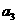 的和
的和 。如果向量
。如果向量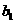 、
、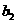 、
、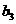 ,满足
,满足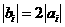 ,且
,且 顺时针旋转
顺时针旋转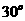 后与
后与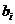 同向,其中
同向,其中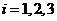 ,则
,则
A.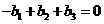 B.
B.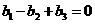
C.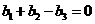 D.
D.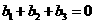
⑽、设 是公差为正数的等差数列,若
是公差为正数的等差数列,若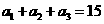 ,
,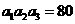 ,则
,则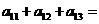
A.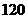 B.
B. C.
C.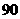 D.
D.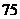
⑾、用长度分别为2、3、4、5、6(单位: )的5根细木棒围成一个三角形(允许连接,但不允许折断),能够得到的三角形的最大面积为
)的5根细木棒围成一个三角形(允许连接,但不允许折断),能够得到的三角形的最大面积为
A.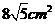 B.
B.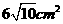 C.
C.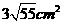 D.
D.
⑿、设集合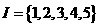 。选择I的两个非空子集A和B,要使B中最小的数大于A中最大的数,则不同的选择方法共有
。选择I的两个非空子集A和B,要使B中最小的数大于A中最大的数,则不同的选择方法共有
A.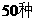 B.
B.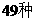 C.
C.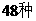 D.
D.
普通高等学校招生全国统一考试
理科数学
第Ⅱ卷
22、解:
(1)
将条件变为:1-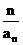 =
=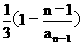 ,因此{1-
,因此{1-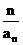 }为一个等比数列,其首项为
}为一个等比数列,其首项为
1-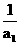 =
=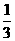 ,公比
,公比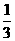 ,从而1-
,从而1-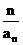 =
=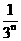 ,据此得an=
,据此得an= (n³1)…………1°
(n³1)…………1°
(2)
证:据1°得,a1·a2·…an=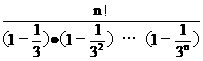
为证a1·a2·……an<2·n!
只要证nÎN*时有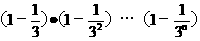 >
>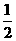 …………2°
…………2°
显然,左端每个因式都是正数,先证明,对每个nÎN*,有
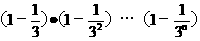 ³1-(
³1-(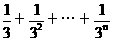 )…………3°
)…………3°
用数学归纳法证明3°式:
(i) n=1时,3°式显然成立,
(ii) 设n=k时,3°式成立,
即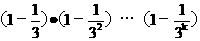 ³1-(
³1-(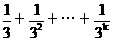 )
)
则当n=k+1时,
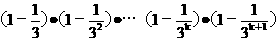 ³(1-(
³(1-(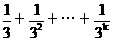 ))·(
))·(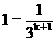 )
)
=1-(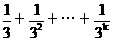 )-
)-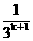 +
+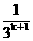 (
(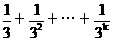 )
)
³1-(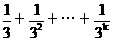 +
+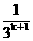 )即当n=k+1时,3°式也成立。
)即当n=k+1时,3°式也成立。
故对一切nÎN*,3°式都成立。
利用3°得,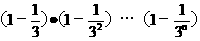 ³1-(
³1-(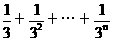 )=1-
)=1-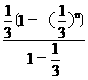
=1-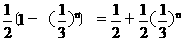 >
>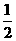
故2°式成立,从而结论成立。
b2(x1-x2)2x+a2(y1-y2)2y=0
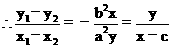
\b2x2+a2y2-b2cx=0…………(3)
2°当AB垂直于x轴时,点P即为点F,满足方程(3)
故所求点P的轨迹方程为:b2x2+a2y2-b2cx=0
(2)因为,椭圆 Q右准线l方程是x=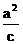 ,原点距l
,原点距l
的距离为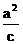 ,由于c2=a2-b2,a2=1+cosq+sinq,b2=sinq(0<q£
,由于c2=a2-b2,a2=1+cosq+sinq,b2=sinq(0<q£ )
)
则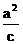 =
=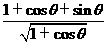 =2sin(
=2sin(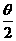 +
+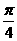 )
)
当q= 时,上式达到最大值。此时a2=2,b2=1,c=1,D(2,0),|DF|=1
时,上式达到最大值。此时a2=2,b2=1,c=1,D(2,0),|DF|=1
设椭圆Q: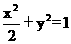 上的点 A(x1,y1)、B(x2,y2),三角形ABD的面积
上的点 A(x1,y1)、B(x2,y2),三角形ABD的面积
S=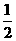 |y1|+
|y1|+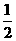 |y2|=
|y2|=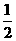 |y1-y2|
|y1-y2|
设直线m的方程为x=ky+1,代入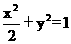 中,得(2+k2)y2+2ky-1=0
中,得(2+k2)y2+2ky-1=0
由韦达定理得y1+y2=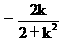 ,y1y2=
,y1y2=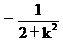 ,
,
4S2=(y1-y2)2=(y1+y2)2-4 y1y2=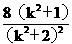
令t=k2+1³1,得4S2=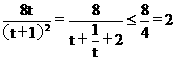 ,当t=1,k=0时取等号。
,当t=1,k=0时取等号。
因此,当直线m绕点F转到垂直x轴位置时,三角形ABD的面积最大。
22、(本大题满分14分)
已知数列{an}满足:a1=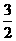 ,且an=
,且an=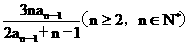
(3) 求数列{an}的通项公式;
(4) 证明:对于一切正整数n,不等式a1·a2·……an<2·n!
21、解:如图,(1)设椭圆Q: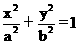 (a>b>0)
(a>b>0)
上的点A(x1,y1)、B(x2,y2),又设P点坐标为P(x,y),则
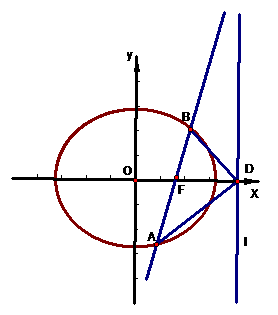
1°当AB不垂直x轴时,x1¹x2,
21、(本大题满分12分)
如图,椭圆Q: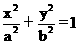 (a>b>0)的右焦点F(c,0),过点F的一动直线m绕点F转动,并且交椭圆于A、B两点,P是线段AB的中点
(a>b>0)的右焦点F(c,0),过点F的一动直线m绕点F转动,并且交椭圆于A、B两点,P是线段AB的中点
(3) 求点P的轨迹H的方程
(4) 在Q的方程中,令a2=1+cosq+sinq,b2=sinq(0<q£ ),确定q的值,使原点距椭圆的右准线l最远,此时,设l与x轴交点为D,当直线m绕点F转动到什么位置时,三角形ABD的面积最大?
),确定q的值,使原点距椭圆的右准线l最远,此时,设l与x轴交点为D,当直线m绕点F转动到什么位置时,三角形ABD的面积最大?
20、解法一:
(1)
方法一:作AH^面BCD于H,连DH。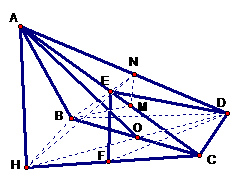
AB^BDÞHB^BD,又AD=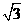 ,BD=1
,BD=1
\AB=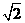 =BC=AC \BD^DC
=BC=AC \BD^DC
又BD=CD,则BHCD是正方形,则DH^BC\AD^BC
方法二:取BC的中点O,连AO、DO
则有AO^BC,DO^BC,\BC^面AOD
\BC^AD
(2)
作BM^AC于M,作MN^AC交AD于N,则ÐBMN就是二面角B-AC-D的平面角,因为AB=AC=BC=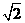 \M是AC的中点,且MN¤¤CD,则BM=
\M是AC的中点,且MN¤¤CD,则BM=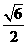 ,MN=
,MN=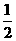 CD=
CD=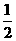 ,BN=
,BN=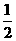 AD=
AD=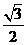 ,由余弦定理可求得cosÐBMN=
,由余弦定理可求得cosÐBMN=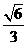
\ÐBMN=arccos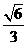
(3)
设E是所求的点,作EF^CH于F,连FD。则EF¤¤AH,\EF^面BCD,ÐEDF就是ED与面BCD所成的角,则ÐEDF=30°。设EF=x,易得AH=HC=1,则CF=x,FD= ,\tanÐEDF=
,\tanÐEDF=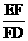 =
=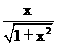 =
=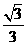 解得x=
解得x=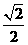 ,则CE=
,则CE=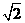 x=1
x=1
故线段AC上存在E点,且CE=1时,ED与面BCD成30°角。
解法二:此题也可用空间向量求解,解答略
20、(本小题满分12分)
如图,在三棱锥A-BCD中,侧面ABD、ACD
是全等的直角三角形,AD是公共的斜边,
且AD=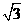 ,BD=CD=1,另一个侧面是正三角形
,BD=CD=1,另一个侧面是正三角形
(4) 求证:AD^BC
(5) 求二面角B-AC-D的大小
(6) 在直线AC上是否存在一点E,使ED与面BCD
成30°角?若存在,确定E的位置;若不存在,说明理由。

