16.把下面不完整的命题补充完整,并使之成为真命题:
若函数 的图象与
的图象与 的图象关于
对称,则函数
的图象关于
对称,则函数 =
=
。
解:若函数 的图象与
的图象与 的图象关于y=x对称, 则函数
的图象关于y=x对称, 则函数 =2x-3.
=2x-3.
(注:填上你认为可以成为真命题的一件情形即可,不必考虑所有可能的情形).
14.非负实数 满足
满足 则x+3y的最大值为
。
则x+3y的最大值为
。
解: 如右图,在同一平面直角坐标系中画出下列
如右图,在同一平面直角坐标系中画出下列
曲线方程的图象:
2x+y-4=0 (x≥0,y≥0)
x+y-3=0 (x≥0,y≥0)
它们分别是线段AB,CD
则非负实数x、y满足的不等式组
 表示的区域为DMAO,令x+3y=b,
表示的区域为DMAO,令x+3y=b,
使直线系x+3y=b通过区域DMAO且使b为取得最大值,当且仅当直线x+3y=b过点D(0,3)这时最大值b=9.
12.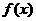 是定义在R上的以3为周期的奇函数,且
是定义在R上的以3为周期的奇函数,且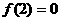 在区间(0,6)内解的个数的最小值是 ( )
在区间(0,6)内解的个数的最小值是 ( )
A.2 B.3 C.4 D.5
解:由题意至少可得f(0)=f(2)=f(-2)=f(3)=f(-3)=f(-5)=f(5)=f(1)=f(4)=0,即在区间(0,6)内f(x)=0的解的个数的最小值是5,选(D)
第Ⅱ卷(非选择题 共90分)
10.已知F1、F2是双曲线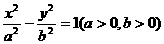 的两焦点,以线段F1F2为边作正三角形MF1F2,若边MF1的中点在双曲线上,则双曲线的离心率是 ( )
的两焦点,以线段F1F2为边作正三角形MF1F2,若边MF1的中点在双曲线上,则双曲线的离心率是 ( )
A.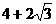 B.
B.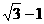 C.
C.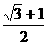 D.
D.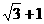
解:设E是正三角形MF1F2的边MF1与双曲线的交点,则点E的坐标为(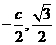 ),代入双曲线方程,并将c=ae代入,整理得e4-8e2+4=0,由e>!,解得e=
),代入双曲线方程,并将c=ae代入,整理得e4-8e2+4=0,由e>!,解得e=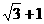 ,选(D)
,选(D)
9.从6人中选4人分别到巴黎、伦敦、悉尼、莫斯科四个城市游览,要求每个城市有一人游览,每人只游览一个城市,且这6人中甲、乙两人不去巴黎游览,则不同的选择方案共有 ( )
A.300种 B.240种 C.144种 D.96种
解:分三种情况:情况一,不选甲、乙两个去游览:则有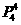 种选择方案,情况二:甲、乙中有一人去游览:有
种选择方案,情况二:甲、乙中有一人去游览:有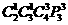 种选择方案;情况三:甲、乙两人都去游览,有
种选择方案;情况三:甲、乙两人都去游览,有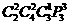 种选择方案,综上不同的选择方案共有
种选择方案,综上不同的选择方案共有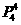 +
+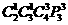 +
+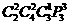 =240,选(B)
=240,选(B)
7.已知p: 则p是q的( )
则p是q的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
解:由 得-1<x<2即x∈(-1,2),由
得-1<x<2即x∈(-1,2),由 得0<x<3,即x∈(0,3),∵(-1,2)不是(0,3)的子集,(0,3)也不是(-1,2)的子集,选(D)
得0<x<3,即x∈(0,3),∵(-1,2)不是(0,3)的子集,(0,3)也不是(-1,2)的子集,选(D)
 8.如图,长方体ABCD-A1B1C1D1中,AA1=AB=2,
8.如图,长方体ABCD-A1B1C1D1中,AA1=AB=2,
AD=1,点E、F、G分别是DD1、AB、CC1的中
点,则异面直线A1E与GF所成的角是( )
A.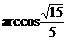 B.
B.
C. D.
D.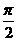
解:∵GB1∥A1E,∠B1GF即为A1E与GF所成的角,B1G=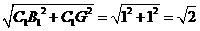
B1F= ,GF=
,GF=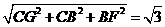 ,B1G2+FG2=B1F2∴
,B1G2+FG2=B1F2∴
∠B1GF=90°,选(D)
4.已知直线m、n与平面 ,给出下列三个命题:
,给出下列三个命题:
①若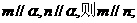
②若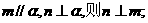
③若
其中真命题的个数是 ( )
A.0 B.1 C.2 D.3
解:②③命题为真命题,选(C)
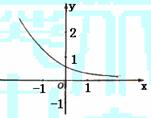 5.函数
5.函数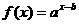 的图象如图,其中a、b为常数,则下列结论正确的是 ( )
的图象如图,其中a、b为常数,则下列结论正确的是 ( )
A.
B.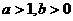
C.
D.
解:从曲线走向可知0<a<1,从曲线位置看,是由y=ax(0<a<1)向左平移|-b|个单位而得到,故-b>0,即b<0,选(D)
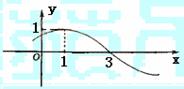 6.函数
6.函数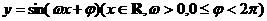 的部分图象如图,则 ( )
的部分图象如图,则 ( )
A.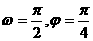 B.
B.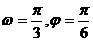
C.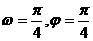 D.
D.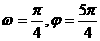
解:由图得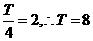 ,由T=
,由T=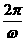 ,得
,得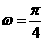 ,在y=sin(
,在y=sin(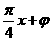 )中令x=1,y=1,得
)中令x=1,y=1,得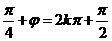 ,
,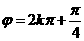 ,得
,得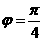 ,选(C)
,选(C)

 .
. =
=
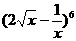 展开式中的常数项是
(用数字作答)。
展开式中的常数项是
(用数字作答)。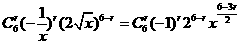 ,令6-3r=0得r=2,故
,令6-3r=0得r=2,故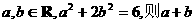 的最小值是 ( )
的最小值是 ( )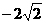 B.
B.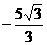 C.-3 D.
C.-3 D.
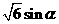 ,b=
,b=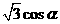 ,则a+b=3sin(
,则a+b=3sin( ),其中
),其中 ,
,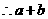 的最小值为-3.选(C)
的最小值为-3.选(C)