(15)(本小题共12分)
已知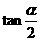 =2,求
=2,求
(I)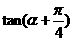 的值; (II)
的值; (II) 的值.
的值.
 (16)(本小题共14分)
(16)(本小题共14分)
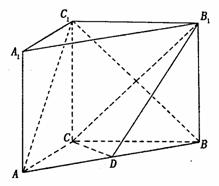
如图, 在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点,
(I)求证:AC⊥BC1;
(II)求证:AC 1//平面CDB1;
(III)求异面直线 AC1与 B1C所成角的余弦值.
(17)数列{an}的前n项和为Sn,且a1=1,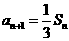 ,n=1,2,3,……,求
,n=1,2,3,……,求
(I)a2,a3,a4的值及数列{an}的通项公式;
(II)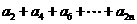 的值.
的值.
(18)(本小题共13分)
甲、乙两人各进行3次射击,甲每次击中目标的概率为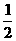 ,乙每次击中目标的概率
,乙每次击中目标的概率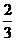 ,
,
(I)甲恰好击中目标的2次的概率;
(II)乙至少击中目标2次的概率;
(III)求乙恰好比甲多击中目标2次的概率.
(19)(本小题共14分)
已知函数f(x)=-x3+3x2+9x+a,
(I)求f(x)的单调递减区间;
(II)若f(x)在区间[-2,2]上的最大值为20,求它在该区间上的最小值.
(20)(本小题共14分)
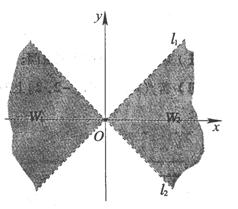
如图,直线 l1:y=kx(k>0)与直线l2:y=-kx之间的阴影区域(不含边界)记为W,其左半部分记为W1,右半部分记为W2.
(I)分别用不等式组表示W1和W2;
(II)若区域W中的动点P(x,y)到l1,l2的距离之积等于d2,求点P的轨迹C的方程;
(III)设不过原点O的直线l与(II)中的曲线C相交于M1,M2两点,且与l1,l2分别交于M3,M4两点.求证△OM1M2的重心与△OM3M4的重心重合.
- 答案

