20.(本小题共14分)
设 是定义在[0,1]上的函数,若存在
是定义在[0,1]上的函数,若存在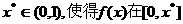 上单调递增,在[x*,1]上单调递减,则称
上单调递增,在[x*,1]上单调递减,则称 为[0,1]上的单峰函数,x*为峰点,包含峰点的区间为含峰区间.
为[0,1]上的单峰函数,x*为峰点,包含峰点的区间为含峰区间.
对任意的[0,1]上的单峰函数 ,下面研究缩短其含峰区间长度的方法.
,下面研究缩短其含峰区间长度的方法.
(Ⅰ)证明:对任意的 为含峰区间;
为含峰区间;
若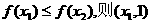 为含峰区间;
为含峰区间;
(Ⅱ)对给定的r(0<r<0.5),证明:存在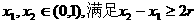 ,使得由(Ⅰ)所确定的含峰区间的长度不大于0.5+r;
,使得由(Ⅰ)所确定的含峰区间的长度不大于0.5+r;
(Ⅲ)选取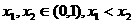 ,由(Ⅰ)可确定含峰区间为(0,
,由(Ⅰ)可确定含峰区间为(0, )或(
)或(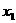 ,1),在所得的含峰区间内选取
,1),在所得的含峰区间内选取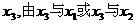 类似地可确定一个新的含峰区间,在第一次确定的含峰区间为(0,
类似地可确定一个新的含峰区间,在第一次确定的含峰区间为(0, )的情况下,试确定
)的情况下,试确定 的值,满足两两之差的绝地值不小于0.02,且使得新的含峰区间的长度缩短到0.34.
的值,满足两两之差的绝地值不小于0.02,且使得新的含峰区间的长度缩短到0.34.
(区间长度等于区间的右端点与左端点之差)
[答案]
[详解]
(I)证明:设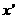 为
为 的峰点,则由单峰函数定义可知
的峰点,则由单峰函数定义可知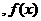 在
在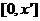 上单调递增,
上单调递增,
在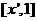 上单调递减.
上单调递减.
当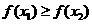 时,假设
时,假设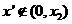 ,则
,则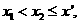 从而
从而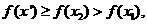
这与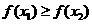 矛盾,所以
矛盾,所以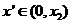 ,即
,即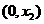 是含峰区间.
是含峰区间.
当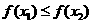 时,假设
时,假设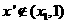 ,则
,则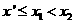 ,从而
,从而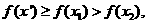
这与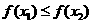 矛盾,所以
矛盾,所以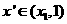 ,即
,即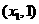 是含峰区间.
是含峰区间.
(II)证明:由(I)的结论可知:
当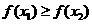 时,含峰区间的长度为
时,含峰区间的长度为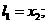
当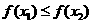 时,含峰区间的长度为
时,含峰区间的长度为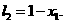
对于上述两种情况,由题意得
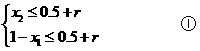
由①得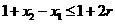 ,即
,即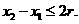
又因为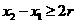 ,所以
,所以

将②代入①得
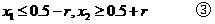
由①和③解得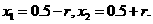
所以这时含峰区间的长度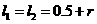 ,即存在
,即存在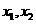 使得所确定的含峰区间
使得所确定的含峰区间
的长度不大于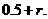
(III)解:对先选择的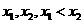 ,由(II)可知
,由(II)可知

在第一次确定的含峰区间为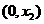 的情况下,
的情况下,  的取值应满足
的取值应满足

由④与⑤可得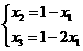
当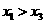 时,含峰区间的长度为
时,含峰区间的长度为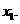
由条件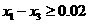 ,得
,得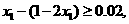 ,从而
,从而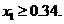
因此,为了将含峰区间的长度缩短到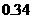 ,只要取
,只要取
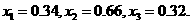
[名师指津]
本题为信息题,通过题目中给出的信息结合已学过的数学知识解决这类问题.
- 答案

